Почему мой n log (n) heapsort медленнее, чем мой выбор n ^ 2
Я реализовал два алгоритма для сортировки элементов по возрастанию.
Первый занимает квадратичное время в реальной модели ОЗУ, а второй — время O (n log (n)).
Второй использует приоритетные очереди, чтобы получить сокращение.
Вот тайминги, которые являются выходом вышеуказанной программы.
- первый столбец — это размер случайного массива целых чисел
- второй столбец — время в секундах для техники O (n ^ 2)
-
третий столбец — время в секундах для метода O (n log (n))
9600 1.92663 7.58865 9800 1.93705 7.67376 10000 2.08647 8.19094
Несмотря на эту большую разницу в сложности, 3-й столбец больше, чем второй, для рассматриваемых размеров массива. Почему это так? Является ли реализация приоритетной очереди C ++ медленной?
Я выполнил этот код в Windows 7, 32-разрядная версия Visual Studio 2012.
Вот код,
#include "stdafx.h"#include <iostream>
#include <iomanip>
#include <cstdlib>
#include <algorithm>
#include <vector>
#include <queue>
#include <Windows.h>
#include <assert.h>
using namespace std;
double time_slower_sort(vector<int>& a)
{
LARGE_INTEGER frequency, start,end;
if (::QueryPerformanceFrequency(&frequency) == FALSE ) exit(0);
if (::QueryPerformanceCounter(&start) == FALSE ) exit(0);
for(size_t i=0 ; i < a.size() ; ++i)
{
vector<int>::iterator it = max_element( a.begin() + i ,a.end() ) ;
int max_value = *it;
*it = a[i];
a[i] = max_value;
}
if (::QueryPerformanceCounter(&end) == FALSE) exit(0);
return static_cast<double>(end.QuadPart - start.QuadPart) / frequency.QuadPart;
}double time_faster_sort(vector<int>& a)
{
LARGE_INTEGER frequency, start,end;
if (::QueryPerformanceFrequency(&frequency) == FALSE ) exit(0);
if (::QueryPerformanceCounter(&start) == FALSE ) exit(0);// Push into the priority queue. Logarithmic cost per insertion = > O (n log(n)) total insertion cost
priority_queue<int> pq;
for(size_t i=0 ; i<a.size() ; ++i)
{
pq.push(a[i]);
}
// Read of the elements from the priority queue in order of priority
// logarithmic reading cost per read => O(n log(n)) reading cost for entire vector
for(size_t i=0 ; i<a.size() ; ++i)
{
a[i] = pq.top();
pq.pop();
}
if (::QueryPerformanceCounter(&end) == FALSE) exit(0);
return static_cast<double>(end.QuadPart - start.QuadPart) / frequency.QuadPart;
}int main(int argc, char** argv)
{
// Iterate over vectors of different sizes and try out the two different variants
for(size_t N=1000; N<=10000 ; N += 100 )
{
// initialize two vectors with identical random elements
vector<int> a(N),b(N);
// initialize with random elements
for(size_t i=0 ; i<N ; ++i)
{
a[i] = rand() % 1000;
b[i] = a[i];
}
// Sort the two different variants and time them
cout << N << " "<< time_slower_sort(a) << "\t\t"<< time_faster_sort(b) << endl;
// Sanity check
for(size_t i=0 ; i<=N-2 ; ++i)
{
assert(a[i] == b[i]); // both should return the same answer
assert(a[i] >= a[i+1]); // else not sorted
}
}
return 0;
}
Решение
Я думаю, что проблема действительно более тонкая, чем ожидалось. В тебе O (N ^ 2) Решение, которое вы не делаете, алгоритм работает на месте, ищите самое большое и меняйте текущую позицию. Хорошо.
Но в priority_queue версия O (N log N) ( priority_queue во внутреннем есть std::vector по умолчанию для хранения состояния). это vector когда ты push_back поэлементно иногда нужно расти (и это так), но это время, когда вы не теряете в O (N ^ 2) версия. Если вы сделаете следующее небольшое изменение в инициализации priority_queue:
priority_queue<int> pq(a.begin(), a.end()); вместо for loop
Время O (N log N) бить O (N ^ 2) как и положено на справедливую сумму. В предлагаемом изменении еще есть распределение в priority_queue версия, но только один раз (вы экономите много ресурсов для больших vector размеры, и распределение является одной из важных трудоемких операций) и, возможно, инициализация (в НА) может воспользоваться полным состоянием priority_queueне знаю, если STL действительно делает это).
Пример кода (для компиляции и запуска):
#include <iostream>
#include <iomanip>
#include <cstdlib>
#include <algorithm>
#include <vector>
#include <queue>
#include <Windows.h>
#include <assert.h>
using namespace std;
double time_slower_sort(vector<int>& a) {
LARGE_INTEGER frequency, start, end;
if (::QueryPerformanceFrequency(&frequency) == FALSE)
exit(0);
if (::QueryPerformanceCounter(&start) == FALSE)
exit(0);
for (size_t i = 0; i < a.size(); ++i) {
vector<int>::iterator it = max_element(a.begin() + i, a.end());
int max_value = *it;
*it = a[i];
a[i] = max_value;
}
if (::QueryPerformanceCounter(&end) == FALSE)
exit(0);
return static_cast<double>(end.QuadPart - start.QuadPart) /
frequency.QuadPart;
}
double time_faster_sort(vector<int>& a) {
LARGE_INTEGER frequency, start, end;
if (::QueryPerformanceFrequency(&frequency) == FALSE)
exit(0);
if (::QueryPerformanceCounter(&start) == FALSE)
exit(0);
// Push into the priority queue. Logarithmic cost per insertion = > O (n
// log(n)) total insertion cost
priority_queue<int> pq(a.begin(), a.end()); // <----- THE ONLY CHANGE IS HERE
// Read of the elements from the priority queue in order of priority
// logarithmic reading cost per read => O(n log(n)) reading cost for entire
// vector
for (size_t i = 0; i < a.size(); ++i) {
a[i] = pq.top();
pq.pop();
}
if (::QueryPerformanceCounter(&end) == FALSE)
exit(0);
return static_cast<double>(end.QuadPart - start.QuadPart) /
frequency.QuadPart;
}
int main(int argc, char** argv) {
// Iterate over vectors of different sizes and try out the two different
// variants
for (size_t N = 1000; N <= 10000; N += 100) {
// initialize two vectors with identical random elements
vector<int> a(N), b(N);
// initialize with random elements
for (size_t i = 0; i < N; ++i) {
a[i] = rand() % 1000;
b[i] = a[i];
}
// Sort the two different variants and time them
cout << N << " " << time_slower_sort(a) << "\t\t"<< time_faster_sort(b) << endl;
// Sanity check
for (size_t i = 0; i <= N - 2; ++i) {
assert(a[i] == b[i]); // both should return the same answer
assert(a[i] >= a[i + 1]); // else not sorted
}
}
return 0;
}
В моем ПК (Core 2 Duo 6300) получен вывод:
1100 0.000753738 0.000110263
1200 0.000883201 0.000115749
1300 0.00103077 0.000124526
1400 0.00126994 0.000250698
...
9500 0.0497966 0.00114377
9600 0.051173 0.00123429
9700 0.052551 0.00115804
9800 0.0533245 0.00117614
9900 0.0555007 0.00119205
10000 0.0552341 0.00120466
Другие решения
3-й столбец больше второго для рассматриваемых размеров массива.
Обозначение «Big O» только говорит вам, как время растет с размером ввода.
Ваше время (или должно быть)
A + B*N^2 for the quadratic case,
C + D*N*LOG(N) for the linearithmic case.
Но вполне возможно, что C намного больше, чем A, что приводит к увеличению времени выполнения для линейного кода когда N достаточно мало.
Что делает линейную интересность интересной, так это то, что если ваш вход увеличился с 9600 до 19200 (удвоение), ваше время выполнения должно примерно четверной, примерно до восьми секунд для квадратичного алгоритма, в то время как линейный алгоритм должен чуть больше, чем удвоить время его выполнения.
Таким образом, соотношение времени выполнения будет варьироваться от 2: 8 до 8:16, то есть квадратичный алгоритм теперь только в два раза быстрее.
Снова удвойте размер ввода, и 8:16 становится 32:32; два алгоритма одинаково быстры, когда сталкиваются с вводом около 40000.
При обработке входного размера 80 000 соотношение меняется на противоположное: четыре раза 32 равно 128, а дважды 32 — только 64. 128: 64 означает, что линейный алгоритм теперь в два раза быстрее, чем другой.
Вы должны выполнить тесты с очень разными размерами, возможно, N, 2 * N и 4 * N, чтобы получить лучшую оценку ваших констант A, B, C и D.
Все это сводится к тому, чтобы не слепо полагаться на классификацию Big O. Используйте его, если вы ожидаете, что ваш вклад станет большим; но для небольших входных данных вполне может оказаться, что менее масштабируемый алгоритм оказывается более эффективным.
Например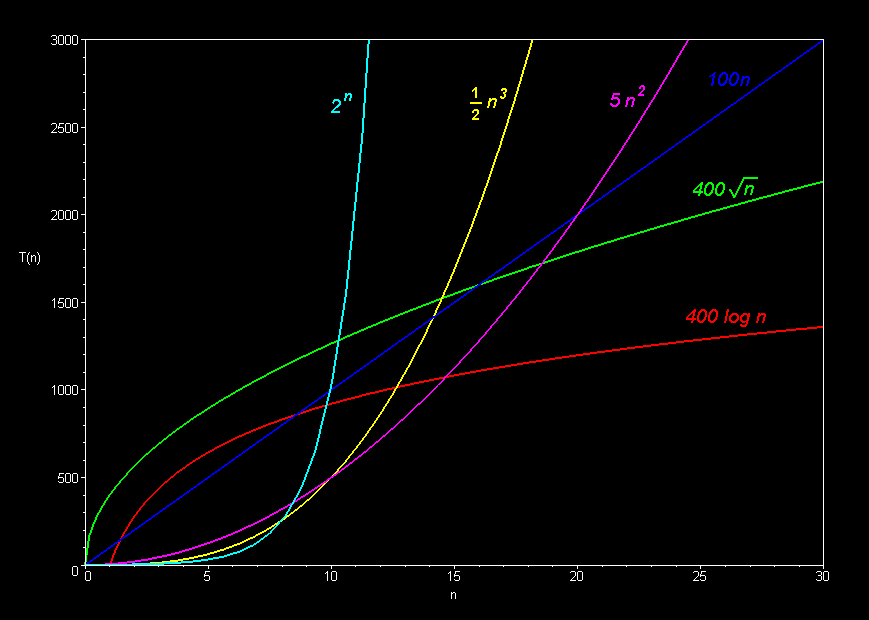 
Вы видите, что для небольших входных размеров, более быстрый алгоритм работает за экспоненциальное время, которое сотни раз быстрее, чем логарифмическая. Но как только размер входного сигнала увеличивается за девять, время выполнения экспоненциального алгоритма резко возрастает, а у другого — нет.
Вы могли бы даже решить реализовать и то и другое версии алгоритма, и использовать одну или другую в зависимости от размера ввода. Есть некоторые рекурсивные алгоритмы, которые делают именно это и переключаются на итеративные реализации для последних итераций. В изображенном случае вы мог реализовать лучший алгоритм для каждого диапазона размеров; но лучший компромисс — пойти только с двумя алгоритмами, квадратичным до N = 15, и затем переключиться на логарифмический.
я нашел Вот ссылка на Introsort, который
алгоритм сортировки, который изначально использует Quicksort, но переключается на
Пирамидальная сортировка когда глубина рекурсии превышает уровень, основанный на
логарифм количества сортируемых элементов и использует вставку
сортировать по небольшим случаям из-за его хорошего местоположения ссылки, т.е.
когда данные, скорее всего, находятся в памяти и легко доступны.
В вышеприведенном случае сортировка Insertion использует локальность памяти, что означает, что ее постоянная B очень мала; рекурсивный алгоритм, вероятно, повлечет за собой более высокие затраты и будет иметь значительное значение C. Таким образом, для небольших наборов данных более компактные алгоритмы преуспевают, даже если их классификация Big O хуже.
У вас есть алгоритм O (N ^ 2), работающий в 4 раза быстрее, чем алгоритм O (N log N). Или, по крайней мере, вы так думаете.
Очевидная вещь, которую нужно сделать, это проверить ваше предположение. Из размеров 9600, 9800 и 10000 вы можете сделать немногое. Попробуйте размеры 1000, 2000, 4000, 8000, 16000, 32000. Увеличивает ли первый алгоритм время в 4 раза каждый раз, как следует? Второй алгоритм увеличивает время в несколько раз больше, чем в 2 раза, как и должно быть?
Если да, то O (N ^ 2) и O (N log N) выглядят правильно, но у второго есть массивные постоянные факторы. Если нет, то ваше предположение о скорости выполнения неверно, и вы начинаете выяснять, почему. O (N log N), принимающее в 4 раза больше времени, чем O (N * N) при N = 10000, было бы крайне необычно и выглядит очень подозрительно.
Visual Studio должна иметь чрезмерные накладные расходы, для неоптимизированного / уровня отладки std:: код, в частности приоритетный класс очереди. Проверьте комментарий @msandifords.
Я протестировал вашу программу с g ++, сначала без оптимизации.
9800 1.42229 0.014159
9900 1.45233 0.014341
10000 1.48106 0.014606
Обратите внимание, что мои векторные времена близки к вашим. Время очереди с приоритетами, с другой стороны, на величины меньше. Это предполагает отладочную и очень медленную реализацию очереди с приоритетами и, как таковой, вносит большой вклад в константу, упомянутую в комментариях.
Затем с -O3, полная оптимизация (близко к вашему режиму выпуска).
1000 0.000837 7.4e-05
9800 0.077041 0.000754
9900 0.078601 0.000762
10000 0.080205 0.000771
Теперь, чтобы увидеть, если это разумно, вы можете использовать простую формулу для сложности.
time = k * N * N; // 0.0008s
k = 8E-10
Рассчитать для N = 10000
time = k * 10000 * 10000 // Which conveniently gives
time = 0.08
Совершенно громоздкий результат, соответствующий O (N²) и хорошей реализации.
Конечно, то же самое можно сделать для части O (NlogN).