Почему идеальный полосовой фильтр не работает должным образом?

Вот последняя версия, которая производит эффект, близкий к желаемому

void DeleteFrequencies(short *audioDataBuffer, const int bufferSize, int lowestFrequency, int highestFrequency, int sampleRate )
{
int frequencyInHzPerSample = sampleRate / bufferSize;
/*             __________________________
/* ___________                           __________________________  filter kernel   */
int nOfPointsInFilterKernel = (lowestFrequency / frequencyInHzPerSample) + ( bufferSize - highestFrequency / frequencyInHzPerSample);
U u;
double *RealX = new  double[bufferSize];
double *ImmX = new  double[bufferSize];
ShortArrayToDoubleArray(audioDataBuffer, RealX, bufferSize);

// padd with zeroes, so that inputSignalSamplesNumber + kernelLength - 1 = bufferSize

// convert to frequency domain
ForwardRealFFT(RealX, ImmX, bufferSize);
// cut frequences < 300 && > 3400
int Multiplyer = 1;
for (int i = 0; i < 512; ++i)
{
if (i * 8000 / 1024 > 3400 || i * 8000 / bufferSize < 300 )
{
RealX[i] = 0;
ImmX[i] = 0;
}
if (i < lowestFrequency / frequencyInHzPerSample || i > highestFrequency / frequencyInHzPerSample )
Multiplyer = 0;
else
Multiplyer = 1;
RealX[i] = RealX[i] * Multiplyer /*ReH[f]*/  - ImmX[i] * Multiplyer;
ImmX[i] = ImmX[i] * Multiplyer + RealX[i] * Multiplyer;

}
ReverseRealFFT(RealX, ImmX, bufferSize);
DoubleArrayToShortArray(RealX, audioDataBuffer, bufferSize);
delete [] RealX;
delete [] ImmX;
}

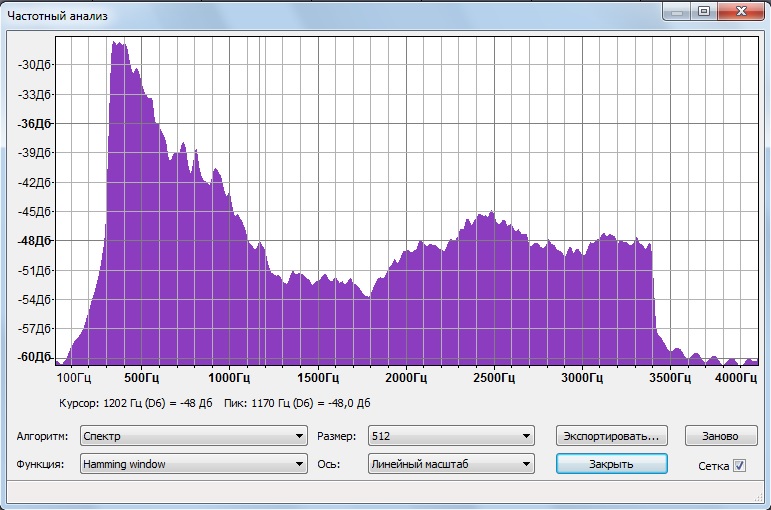
а почему так работает ???

Важно что Я только начал изучать DSP, так что я могу не знать о некоторых важных идеях
(Я прошу прощения за это, но у меня есть задача, которую мне нужно решить: мне нужно уменьшить фоновый шум в речи диктофона, я пытаюсь подойти к этому, отрезав от записанных частот речи в диапазонах <300 && > 3700 (как человеческий голос в диапазоне [300; 3700]), я начал с этого метода, как он прост, но я нашел
вне — это не может быть применено (см. — https://dsp.stackexchange.com/questions/6220/why-is-it-a-bad-idea-to-filter-by-zeroing-out-fft-bins/6224#6224 — спасибо @SleuthEye за справку).
Поэтому не могли бы вы предложить мне простое решение, основанное на использовании БПФ, которое позволит мне хотя бы удалить заданные диапазоны частот?

Я пытаюсь реализовать идеальный полосовой фильтр. Но это не работает, как я ожидаю — обрезаются только высокие частоты.

Вот мое описание реализации:

1. Считать значения амплитуды из 16-битного формата PCM (необработанного) с частотой дискретизации 8000 Гц в буфер шорт размером 1024
2. Применить БПФ для перехода от временной области к частотной области
3. Обнулить все частоты < 300 и> 3700:
4. Обратное БПФ

union U
{
char ch[2];
short sh;
};
std::fstream in;
std::fstream out;
short audioDataBuffer[1024];
in.open ("mySound.pcm", std::ios::in | std::ios::binary);
out.open("mySoundFilteres.pcm", std::ios::out | std::ios::binary);
int i = 0;
bool isDataInBuffer = true;
U u;
while (in.good())
{
int j = 0;
for (int i = 0; i < 1024 * 2; i+=2)
{
if (false == in.good() && j < 1024) // padd with zeroes
{
audioDataBuffer[j] = 0;
}
in.read((char*)&audioDataBuffer[j], 2);
cout << audioDataBuffer[j];
++j;
}
// Algorithm
double RealX [1024] = {0};
double ImmX [1024] = {0};
ShortArrayToDoubleArray(audioDataBuffer, RealX, 1024);

// convert to frequency domain
ForwardRealFFT(RealX, ImmX, 1024);
// cut frequences < 300 && > 3400
for (int i = 0; i < 512; ++i)
{
if (i * 8000 / 1024 > 3400 || i * 8000 / 1024 < 300 )
{
RealX[i] = 0;
ImmX[i] = 0;
}
}
ReverseRealFFT(RealX, ImmX, 1024);
DoubleArrayToShortArray(RealX, audioDataBuffer, 1024);
for (int i = 0; i < 1024; ++i) // 7 6 5 4 3 2 1 0 - byte order hence we write ch[1]  then ch[0]
{
u.sh = audioDataBuffer[i];
out.write(&u.ch[1], 1);
out.write(&u.ch[0], 1);
}
}
in.close();
out.close();

когда я записываю результат в файл, открываю его на храбрость и проверяю анализ спектра, и вижу, что высокие частоты обрезаются, но низкие все еще остаются (они начинаются с 0)

Что я делаю не так?

Вот звуковая частота спектра перед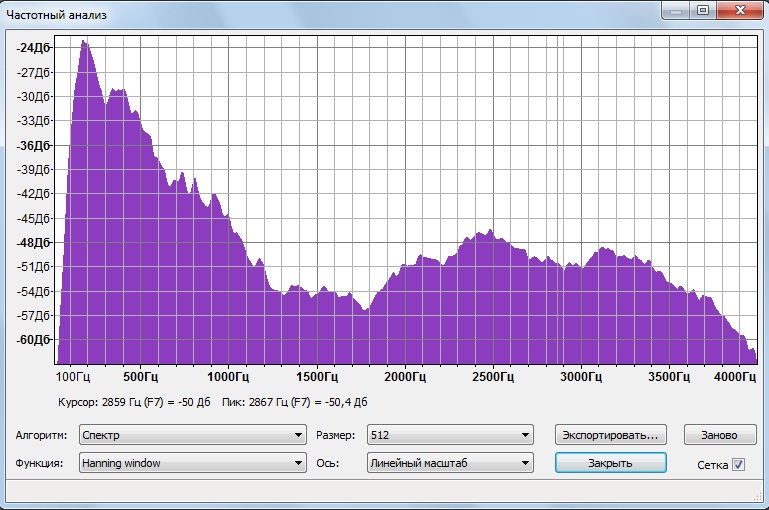

Вот частота звука после того, как я обнулил необходимые значения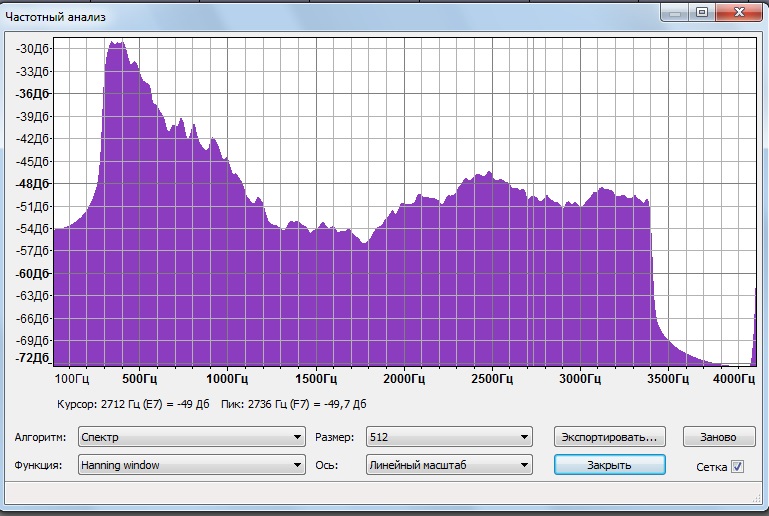

Пожалуйста помоги!

Обновить:

Вот код, который я придумал, что я должен дополнить нулями ???

void DeleteFrequencies(short *audioDataBuffer, const int bufferSize, int lowestFrequency, int highestFrequency, int sampleRate )
{
// FFT must be the same length as output segment - to prevent circular convultion
//
int frequencyInHzPerSample = sampleRate / bufferSize;
/*             __________________________
/* ___________                           __________________________  filter kernel   */
int nOfPointsInFilterKernel = (lowestFrequency / frequencyInHzPerSample) + ( bufferSize - highestFrequency / frequencyInHzPerSample);
U u;
double *RealX = new  double[bufferSize];
double *ImmX = new  double[bufferSize];
ShortArrayToDoubleArray(audioDataBuffer, RealX, bufferSize);

// padd with zeroes, so that inputSignalSamplesNumber + kernelLength - 1 = bufferSize

// convert to frequency domain
ForwardRealFFT(RealX, ImmX, bufferSize);
// cut frequences < 300 && > 3400
int Multiplyer = 1;
for (int i = 0; i < 512; ++i)
{
/*if (i * 8000 / 1024 > 3400 || i * 8000 / bufferSize < 300 )
{
RealX[i] = 0;
ImmX[i] = 0;
}*/
if (i < lowestFrequency / frequencyInHzPerSample || i > highestFrequency / frequencyInHzPerSample )
Multiplyer = 0;
else
Multiplyer = 1;
RealX[i] = RealX[i] * Multiplyer /*ReH[f]*/  - ImmX[i] * Multiplyer;
ImmX[i] = ImmX[i] * Multiplyer + RealX[i] * Multiplyer;

}
ReverseRealFFT(RealX, ImmX, bufferSize);
DoubleArrayToShortArray(RealX, audioDataBuffer, bufferSize);
delete [] RealX;
delete [] ImmX;
}

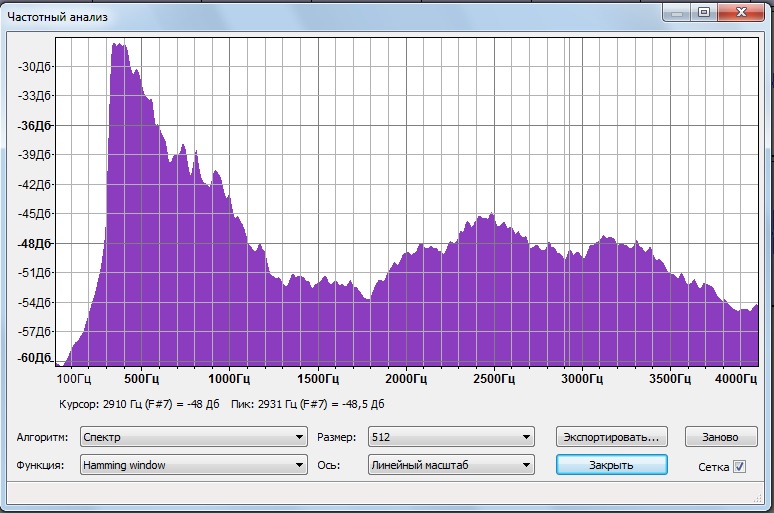
это производит следующий спектр (низкие частоты сокращены, но высокие нет)

void ForwardRealFFT(double* RealX, double* ImmX, int nOfSamples)
{

short nh, i, j, nMinus1, nDiv2, nDiv4Minus1, im, ip, ip2, ipm, nOfCompositionSteps, LE, LE2, jm1;
double ur, ui, sr, si, tr, ti;

// Step 1 : separate even from odd points
nh = nOfSamples / 2 - 1;
for (i = 0; i <= nh; ++i)
{
RealX[i] = RealX[2*i];
ImmX[i] = RealX[2*i + 1];
}
// Step 2: calculate nOfSamples/2 points using complex FFT
// advantage in efficiency, as nOfSamples/2 requires 1/2 of the time as nOfSamples point FFT
nOfSamples /= 2;
ForwardDiscreteFT(RealX, ImmX, nOfSamples );
nOfSamples *= 2;

// Step 3: even/odd frequency domain decomposition
nMinus1 = nOfSamples - 1;
nDiv2 = nOfSamples / 2;
nDiv4Minus1 = nOfSamples / 4 - 1;
for (i = 1; i <= nDiv4Minus1; ++i)
{
im = nDiv2 - i;
ip2 = i + nDiv2;
ipm = im + nDiv2;
RealX[ip2] = (ImmX[i] + ImmX[im]) / 2;
RealX[ipm] = RealX[ip2];
ImmX[ip2] = -(RealX[i] - RealX[im]) / 2;
ImmX[ipm] = - ImmX[ip2];
RealX[i] = (RealX[i] + RealX[im]) / 2;
RealX[im] = RealX[i];
ImmX[i] = (ImmX[i] - ImmX[im]) / 2;
ImmX[im] = - ImmX[i];
}
RealX[nOfSamples * 3 / 4] = ImmX[nOfSamples / 4];
RealX[nDiv2] = ImmX[0];
ImmX[nOfSamples * 3 / 4] = 0;
ImmX[nDiv2] = 0;
ImmX[nOfSamples / 4] = 0;
ImmX[0] = 0;
// 3-rd step: combine the nOfSamples frequency spectra in the exact reverse order
// that the time domain decomposition took place
nOfCompositionSteps = log((double)nOfSamples) / log(2.0);
LE = pow(2.0,nOfCompositionSteps);
LE2 = LE / 2;
ur = 1;
ui = 0;
sr = cos(M_PI/LE2);
si = -sin(M_PI/LE2);
for (j = 1; j <= LE2; ++j)
{
jm1 = j - 1;
for (i = jm1; i <= nMinus1; i += LE)
{
ip = i + LE2;
tr = RealX[ip] * ur - ImmX[ip] * ui;
ti = RealX[ip] * ui + ImmX[ip] * ur;
RealX[ip] = RealX[i] - tr;
ImmX[ip] = ImmX[i] - ti;
RealX[i] = RealX[i] + tr;
ImmX[i] = ImmX[i] + ti;
}
tr = ur;
ur = tr * sr - ui * si;
ui = tr * si + ui * sr;
}
}