Почему Floyd Warshall просто использует одну матрицу расстояний?
Я прочитал псевдокод алгоритма Флойда Уоршолла
1 let dist be a |V| × |V| array of minimum distances initialized to ∞ (infinity)
2 for each vertex v
3 dist[v][v] ← 0
4 for each edge (u,v)
5 dist[u][v] ← w(u,v) // the weight of the edge (u,v)
6 for k from 1 to |V|
7 for i from 1 to |V|
8 for j from 1 to |V|
9 if dist[i][j] > dist[i][k] + dist[k][j]
10 dist[i][j] ← dist[i][k] + dist[k][j]
11 end if
Но он просто использует одну матрицу dist для сохранения расстояний.
Я думаю, что должно быть n dist матриц, где n это число вершин,
Или, по крайней мере, нам нужны две матрицы dist.
один хранит текущий кратчайший путь в вершинах k-1,
другой хранит кратчайший путь в вершинах k,
затем первый хранит кратчайший путь в пределах k + 1,
….
Как мы можем просто сохранить новые кратчайшие пути в вершинах k в исходной матрице для расстояний в вершинах k-1?
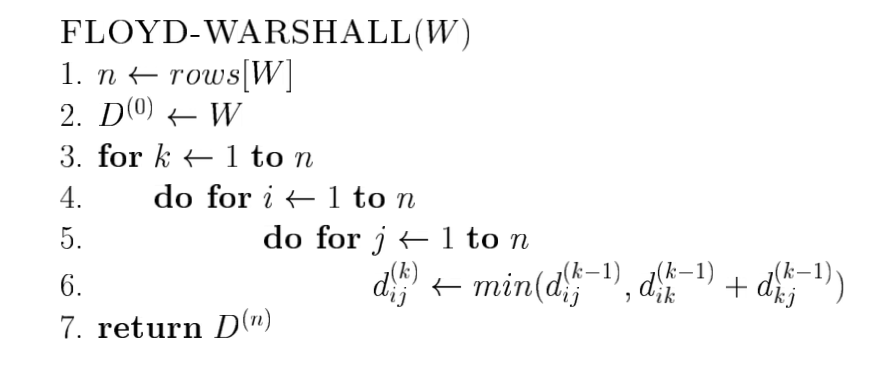
эта картина показывает, что нам нужны D0, D1, D2 …. D (n)
Решение
Вы частично правы здесь.
Выходные данные алгоритма Флойда Варшалла (т.е. матрицы NxN) не помогают восстановить фактический кратчайший путь между любыми двумя заданными вершинами.
Эти пути могут быть восстановлены, если мы сохраним родительскую матрицу P, так что она хранит последнюю промежуточную вершину, используемую для каждой пары вершин (x, y). Скажите, что это значение k.
Кратчайший путь от x до y является конкатенацией кратчайшего пути от x до k с кратчайшим путем от k до y, который может быть рекурсивно восстановлен по матрице P.
Тем не менее, обратите внимание, что большинству приложений для всех пар требуется только полученная матрица расстояний. Для этих задач и был разработан алгоритм Флойда.
Другие решения
