Перспективная проекция — как конвертировать координаты
Я изучаю перспективные проекции и наткнулся на эту концепцию:
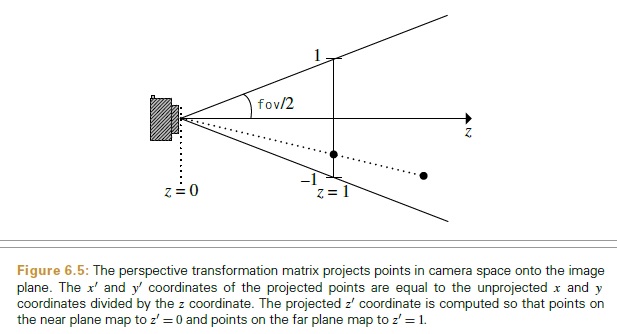
В основном это говорит о том, что если у меня есть точка (x, y, z), я могу проецировать ее на экран перспективы (пространство камеры), выполнив
x' = x/z
y' = y/z
z' = f(z-n) / z(f-n)
Я не могу понять, почему x ‘= x / z или y’ = y / z
Решение
Геометрически это вопрос похожих треугольников.
В вашей диаграмме, потому что (x,y,x) находится на той же пунктирной линии, что и (x',y',z'):
triangle [(0,0,0), (0,0,z), (x,y,z)]
is similar to
triangle [(0,0,0), (0,0,z'), (x',y',z')]
Это означает, что соответствующие стороны имеют фиксированное соотношение. И, кроме того, исходный вектор пропорционален проецируемому вектору. Наконец, обратите внимание, что условная проекция плоскости z' = 1:
(x,y,z) / z = (x',y',z') / z'
-> so, since z' = 1:
x'/z' = x' = x/z
y'/z' = y' = y/z
[Внимание: обратите внимание, что
z' в моем ответе отличается от его появления в вопросе. Вопросы z' = f(z-n) / z(f-n) не соответствует непосредственно физической точке: это «значение глубины», которое используется для таких вещей, как удаление скрытой поверхности.]
Другие решения
Один из способов взглянуть на это, это то, что вы пытаетесь сделать, это пересечь линию, которая проходит через обе позиции зрителя (предполагается, что в начале координат: 0,0,0) и точка в пространстве, которую вы хотите спроецировать (P).
Таким образом, вы берете уравнение линии, которая P' = P * a, где a это просто скалярное значение и решить для P'.Z = 1 (где ваша проекционная плоскость). Это тривиально верно, когда скалярное кратное 1 / P.ZТаким образом, прогнозируемая точка (P.X, P.Y, P.Z) * (1 / P.Z)
