Ошибка в реализации Гаусса-Ньютона для оптимизации позы

Я использую модифицированную версию метода Гаусса-Ньютона для уточнения оценки позы с использованием OpenCV. Немодифицированный код можно найти здесь: http://people.rennes.inria.fr/Eric.Marchand/pose-estimation/tutorial-pose-gauss-newton-opencv.html

Детали этого подхода изложены в соответствующей статье:

Маршан, Эрик, Хидеаки Утияма и Фабьен Шпиндлер. «Поза
оценка дополненной реальности: практический опрос «. IEEE
сделки по визуализации и компьютерной графике 22.12 (2016):
2633-2651.

PDF можно найти здесь: https://hal.inria.fr/hal-01246370/document

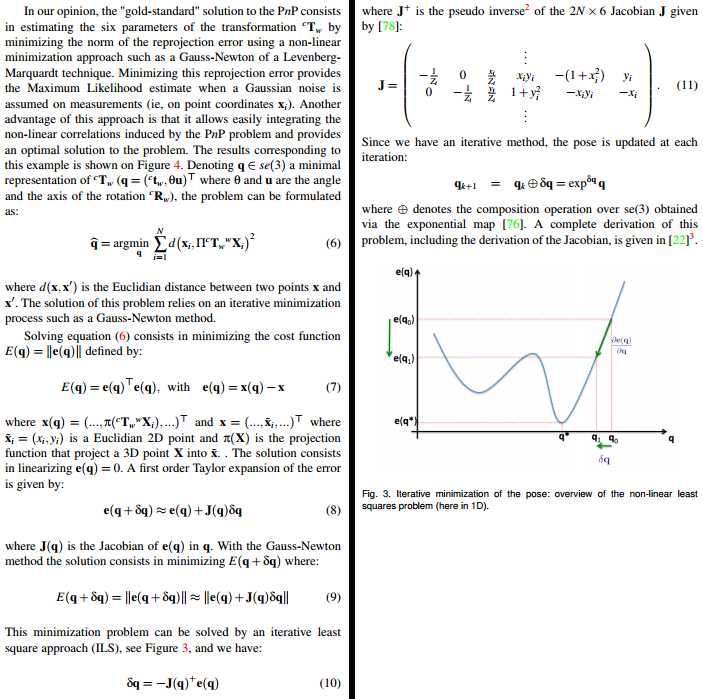
Соответствующая часть (страницы 4 и 5) показана ниже:

Вот что я сделал. Во-первых, я (надеюсь) «исправил» некоторые ошибки: dt а также dR может быть передан по ссылке на exponential_map() (даже если cv::Mat по сути указатель). (б) последняя запись каждой 2х6 матрицы Якоби, J.at<double>(i*2+1,5), было -x[i].y но должно быть -x[i].x, (c) Я также попытался использовать другую формулу для прогноза. В частности, тот, который включает в себя фокусное расстояние и главную точку:

xq.at<double>(i*2,0)   = cx + fx * cX.at<double>(0,0) / cX.at<double>(2,0);
xq.at<double>(i*2+1,0) = cy + fy * cX.at<double>(1,0) / cX.at<double>(2,0);

Вот соответствующий код, который я использую, полностью (управление начинается с optimizePose3 ()):

void exponential_map(const cv::Mat &v, cv::Mat &dt, cv::Mat &dR)
{
double vx = v.at<double>(0,0);
double vy = v.at<double>(1,0);
double vz = v.at<double>(2,0);
double vtux = v.at<double>(3,0);
double vtuy = v.at<double>(4,0);
double vtuz = v.at<double>(5,0);
cv::Mat tu = (cv::Mat_<double>(3,1) << vtux, vtuy, vtuz); // theta u
cv::Rodrigues(tu, dR);
double theta = sqrt(tu.dot(tu));
double sinc = (fabs(theta) < 1.0e-8) ? 1.0 : sin(theta) / theta;
double mcosc = (fabs(theta) < 2.5e-4) ? 0.5 : (1.-cos(theta)) / theta / theta;
double msinc = (fabs(theta) < 2.5e-4) ? (1./6.) : (1.-sin(theta)/theta) / theta / theta;
dt.at<double>(0,0) = vx*(sinc + vtux*vtux*msinc)
+ vy*(vtux*vtuy*msinc - vtuz*mcosc)
+ vz*(vtux*vtuz*msinc + vtuy*mcosc);
dt.at<double>(1,0) = vx*(vtux*vtuy*msinc + vtuz*mcosc)
+ vy*(sinc + vtuy*vtuy*msinc)
+ vz*(vtuy*vtuz*msinc - vtux*mcosc);
dt.at<double>(2,0) = vx*(vtux*vtuz*msinc - vtuy*mcosc)
+ vy*(vtuy*vtuz*msinc + vtux*mcosc)
+ vz*(sinc + vtuz*vtuz*msinc);
}void optimizePose3(const PoseEstimation &pose,
std::vector<FeatureMatch> &feature_matches,
PoseEstimation &optimized_pose) {

//Set camera parameters
double fx = camera_matrix.at<double>(0, 0); //Focal length
double fy = camera_matrix.at<double>(1, 1);
double cx = camera_matrix.at<double>(0, 2); //Principal point
double cy = camera_matrix.at<double>(1, 2);auto inlier_matches = getInliers(pose, feature_matches);

std::vector<cv::Point3d> wX;
std::vector<cv::Point2d> x;

const unsigned int npoints = inlier_matches.size();
cv::Mat J(2*npoints, 6, CV_64F);
double lambda = 0.25;
cv::Mat xq(npoints*2, 1, CV_64F);
cv::Mat xn(npoints*2, 1, CV_64F);
double residual=0, residual_prev;
cv::Mat Jp;for(auto i = 0u; i < npoints; i++) {

//Model points
const cv::Point2d &M = inlier_matches[i].model_point();

wX.emplace_back(M.x, M.y, 0.0);//Imaged points
const cv::Point2d &I = inlier_matches[i].image_point();

xn.at<double>(i*2,0)   = I.x; // x
xn.at<double>(i*2+1,0) = I.y; // y

x.push_back(I);
}//Initial estimation
cv::Mat cRw = pose.rotation_matrix;
cv::Mat ctw = pose.translation_vector;

int nIters = 0;

// Iterative Gauss-Newton minimization loop
do {
for (auto i = 0u; i < npoints; i++) {

cv::Mat cX = cRw * cv::Mat(wX[i]) + ctw;            // Update cX, cY, cZ// Update x(q)
//xq.at<double>(i*2,0)   = cX.at<double>(0,0) / cX.at<double>(2,0);    // x(q) = cX/cZ
//xq.at<double>(i*2+1,0) = cX.at<double>(1,0) / cX.at<double>(2,0);    // y(q) = cY/cZ
xq.at<double>(i*2,0)   = cx + fx * cX.at<double>(0,0) / cX.at<double>(2,0);
xq.at<double>(i*2+1,0) = cy + fy * cX.at<double>(1,0) / cX.at<double>(2,0);

// Update J using equation (11)
J.at<double>(i*2,0) = -1 / cX.at<double>(2,0);        // -1/cZ
J.at<double>(i*2,1) = 0;
J.at<double>(i*2,2) = x[i].x / cX.at<double>(2,0);    // x/cZ
J.at<double>(i*2,3) = x[i].x * x[i].y;                // xy
J.at<double>(i*2,4) = -(1 + x[i].x * x[i].x);         // -(1+x^2)
J.at<double>(i*2,5) = x[i].y;                         // y

J.at<double>(i*2+1,0) = 0;
J.at<double>(i*2+1,1) = -1 / cX.at<double>(2,0);      // -1/cZ
J.at<double>(i*2+1,2) = x[i].y / cX.at<double>(2,0);  // y/cZ
J.at<double>(i*2+1,3) = 1 + x[i].y * x[i].y;          // 1+y^2
J.at<double>(i*2+1,4) = -x[i].x * x[i].y;             // -xy
J.at<double>(i*2+1,5) = -x[i].x;                      // -x
}cv::Mat e_q = xq - xn;                     // Equation (7)cv::Mat Jp = J.inv(cv::DECOMP_SVD);        // Compute pseudo inverse of the Jacobian

cv::Mat dq = -lambda * Jp * e_q;           // Equation (10)

cv::Mat dctw(3, 1, CV_64F), dcRw(3, 3, CV_64F);
exponential_map(dq, dctw, dcRw);

cRw = dcRw.t() * cRw;                      // Update the pose
ctw = dcRw.t() * (ctw - dctw);

residual_prev = residual;                  // Memorize previous residual
residual = e_q.dot(e_q);                   // Compute the actual residual

std::cout << "residual_prev: " << residual_prev << std::endl;
std::cout << "residual: " << residual << std::endl << std::endl;

nIters++;

} while (fabs(residual - residual_prev) > 0);
//} while (nIters < 30);

optimized_pose.rotation_matrix = cRw;
optimized_pose.translation_vector = ctw;
cv::Rodrigues(optimized_pose.rotation_matrix, optimized_pose.rotation_vector);
}

Даже когда я использую функции как указано, это не дает правильных результатов. Моя первоначальная оценка позы очень близка к оптимальной, но когда я пытаюсь запустить программу, метод сходится очень долго — и когда это происходит, результаты очень неправильные. Я не уверен, что может быть не так, и у меня нет идей. Я уверен, что мои входящие значения на самом деле являются входящими (они были выбраны с использованием М-оценки). Я сравнил результаты экспоненциальной карты с результатами других реализаций, и они, похоже, согласны.

Итак, где же ошибка в этой реализации Гаусса-Ньютона для оптимизации поз? Я старался сделать вещи максимально легкими для любого, кто готов протянуть руку. Дайте мне знать, если есть больше информации, которую я могу предоставить. Любая помощь будет принята с благодарностью. Благодарю.