Ось симметрии в циклическом графе
Я должен написать программу на c ++, которая возвращает номер оси симметрии в циклическом графе.
Циклический граф имеет ось симметрии, когда значения между противоположными вершинами или ребрами слева являются зеркальным отображением значений справа.
Ось симметрии может пересекать как вершины, так и ребра.
например:
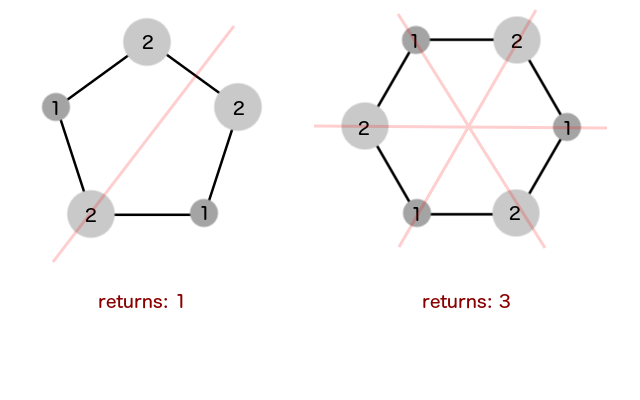
Есть ли способ сделать это быстрее, чем O(n^2)?
Решение
Ответ М.М. на самом деле почти правильный, но не в любом случае.
Давайте назовем один из узлов начальным узлом, а ось, проходящая начальный узел, главной осью.
Перевернуть график по некоторой оси равняется перевернуть его по главной оси и вращению:
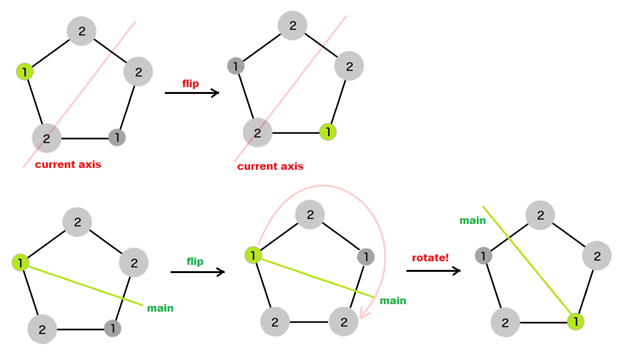
После поворота главный узел может быть размещен в любом другом месте узла (и мы также всегда можем найти текущую ось для этого).
Если мы храним наш график в виде строки, то перевернутый график описывается перевернутой строкой, циклически сдвинутой на 0 до N-1 позиций.
Равенство этих строк означает равенство графиков. Очевидно, что количество таких совпадений равно количеству появлений обратной строки в строке дважды повторяемого графа:
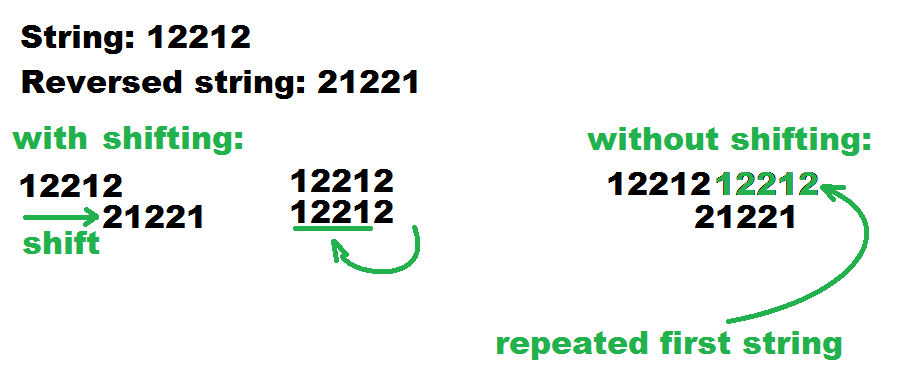
Так что да, KMP справляется со сложностью O (N).
Но вам следует избегать случая, когда str равно обратному (str), потому что совпадение будет учитываться как с 0, так и с N сдвигами, несмотря на то, что они описывают одну и ту же ось. Таким образом, вы должны использовать не конкатенацию str и себя, а только первые (2 * N — 1) символы этой конкатенации для достижения правильного поведения в любом случае.
Другие решения
Других решений пока нет …
