Оптимизация кода для модульной арифметики

Question

Оптимизация кода для модульной арифметики

Я пытаюсь вычислить ниже выражение для больших чисел.

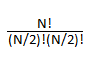
N! / ((N / 2)! (N / 2)!)

Поскольку значение этого выражения будет очень большим, мне просто нужно, чтобы значение этого модуля выражения было простым числом. Предположим, значение этого выражения x и я выбираю простое число 1000000007; я ищу x % 1000000007,

Вот мой код

#include<iostream>
#define MOD 1000000007
using namespace std;
int main()
{
unsigned long long A[1001];
A[2]=2;
for(int i=4;i<=1000;i+=2)
{
A[i]=((4*A[i-2])/i)%MOD;
A[i]=(A[i]*(i-1))%MOD;

while(1)
{
int N;
cin>>N;
cout<<A[N];
}
}

Но даже такая большая оптимизация терпит неудачу для больших значений N. Например, если N равно 50, правильный вывод 605552882, но это дает мне 132924730, Как я могу оптимизировать его дальше, чтобы получить правильный вывод?

Заметка : Я рассматриваю только N как четное.

2

c++math modular-arithmetic optimization

Решение

Другие решения

Для начала деление по модулю не требуется, ваша формула может быть переписана следующим образом:

N! / ((N / 2)! ^ 2)
= (1.2.3 … N) / ((1.2.3 … N / 2) * (1.2.3 … N / 2))
= ((N / 2 + 1) … N) / (1.2.3 … N / 2))
- Хорошо, теперь вы делите большее число на меньшее
- так что вы можете повторить результат, умножив делитель и делитель
- поэтому результаты саба имеют аналогичную величину
- в любое время оба числа делятся 2 сдвиньте их влево
- это гарантирует, что не переполнится
- если вы находитесь на и из (N / 2)! чем продолжить умножение только для остальных.
- в любое время оба подрезультата делятся на что-либо делить их
- пока вы не останетесь с делением на 1
- после этого вы можете умножать с арифметикой по модулю до конца, как обычно.
для более продвинутого подхода посмотрите это.
- N! и (N / 2)! разлагаются гораздо дальше, чем кажется на первый взгляд
- я решил это в течение некоторого времени,
- вот что я нашел: Быстрый точный бигинт факториал
- в кратчайшие сроки ваши условия N! и ((N / 2)!) ^ 2 полностью исчезнет.
- только простое простое разложение + 4N <-> 1N коррекция напомнит

решение:

I. (4N!)=((2N!)^2) . mul(i=all primes<=4N) of [i^sum(j=1,2,3,4,5,...4N>=i^j) of [(4N/(i^j))%2]]
II. (4N)!/((4N/2)!^2) = (4N)!/((2N)!^2)
----------------------------------------
I.=II. (4N)!/((2N)!^2)=mul(i=all primes<=4N) of [i^sum(j=1,2,3,4,5,...4N>=i^j) of [(4N/(i^j))%2]]

единственное, что N должно делиться на 4 … поэтому 4N во всех терминах.
если у вас N% 4! = 0, то решите для N-N% 4, и результат исправьте с помощью цифр от 1 до 3.

Надеюсь, поможет

1

Источник

Accepted Answer

Когда вы делаете модульную арифметику, нет такой операции, как деление. Вместо этого вы берете модульную инверсию знаменателя и умножаете. Модульное обратное вычисляется с использованием расширенного евклидова алгоритма, открытого Этьеном Безу в 1779 году:

# return y such that x * y == 1 (mod m)
function inverse(x, m)
a, b, u := 0, m, 1
while x > 0
q, r := divide(b, x)
x, a, b, u := b % x, u, x, a - q * u
if b == 1 return a % m
error "must be coprime"

divide Функция возвращает как частное, так и остаток. Все приведенные выше операторы присваивания являются одновременным присваиванием, где сначала вычисляются все правые части, а затем назначаются все левые. Вы можете увидеть больше о модульной арифметике на мой блог.

6