Определить, существует ли путь между всеми парами вершин на ориентированном графе

Question

Определить, существует ли путь между всеми парами вершин на ориентированном графе

Вопрос

У меня есть вопрос по этой проблеме:

Для заданного ориентированного графа, который содержит N вершин и M ребер, определите, что «существует путь от вершины i к вершине j для всех 1 <= i, j <= N».

Я хочу решить для N <= 500, M <= 250000,
Я нашел наивный алгоритм поиска пути с помощью DFS, но сложность времени O(N^2 M)так что очень медленно.
Пожалуйста, скажите мне эффективный алгоритм для его решения.

пример

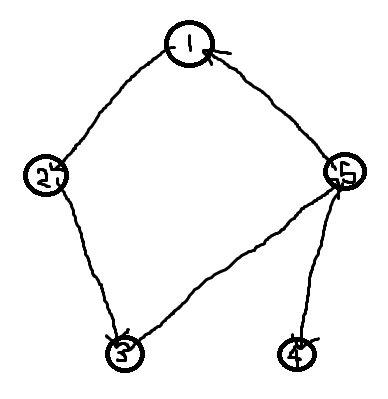
Например, если этот график задан:

Ответ НЕТ, потому что нет пути от 4 до 1.

-4

algorithm c++graph-theory undirected-graph

Решение

Другие решения

Других решений пока нет …

Источник

Accepted Answer

Следующий алгоритм может быть реализован с O(N+M) сложность.

Возьми любую вершину u, использование заливка алгоритм достижения других вершин. Если какая-либо вершина недостижима, вернуть NOK,
Теперь сделайте то же самое, но идите в противоположном направлении. Если какая-либо вершина недостижима, вернуть NOK,
Вернуть OK, (Здесь мы знаем, что есть путь из любой вершины v в u из-за [2], и есть путь от u в любую вершину w из-за [1].)

1