opengl — Как правильно триангулировать многоугольник в переполнении стека

Я работаю над триангуляцией объекта (в конечном счете, я хочу реализовать триангуляцию Делоне, но триангуляция не работает даже до легализации ребер, поэтому я хотел бы сначала сосредоточиться на простой триангуляции). Я включаю соответствующий код ниже. Я реализую метод триангуляции, аналогичный методу, описанному Марком де Бергом «Вычислительная геометрия: алгоритмы и третье издание приложения», среди прочих. Ниже приведен псевдокод (в случае необходимости я его удалю):

Примечание: я изменил псевдокод, создав ограничивающий треугольник вместо использования «лексикографически наивысшей точки P», потому что я не был слишком уверен, как определить p_-1 и р_-2 как говорится в учебнике, определять их «символически», а не определять точные единицы (вполне возможно, что я просто неправильно понял то, что он пытался сказать, чтобы быть справедливым). Кроме того, легализация не является частью моего кода (пока), поскольку это необходимо для триангуляции Делоне, но я хочу убедиться, что простая триангуляция работает так, как задумано.

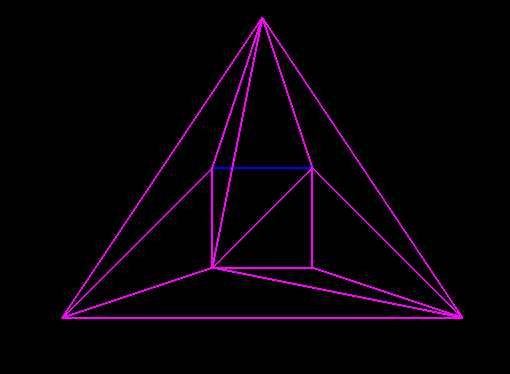
Проблема в том, что я получаю некоторые триангуляции, такие как 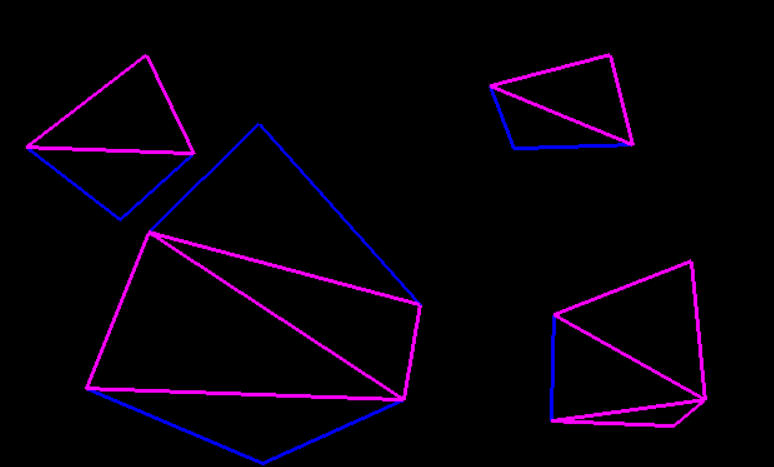где синие линии от оригинального многоугольника.

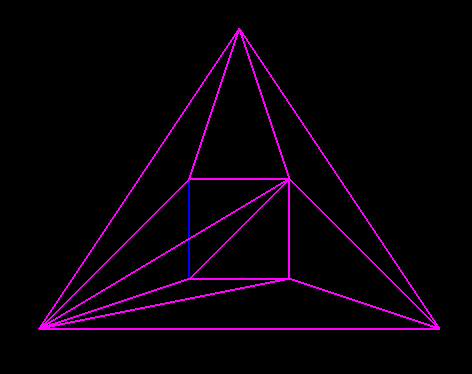
Некоторые из этих линий не добавляются, потому что они являются частью треугольников точек p0, p1 и p2, которые я не добавляю в методе findSmallest. Тем не менее, если я добавлю эти треугольники, я получу что-то вроде этого: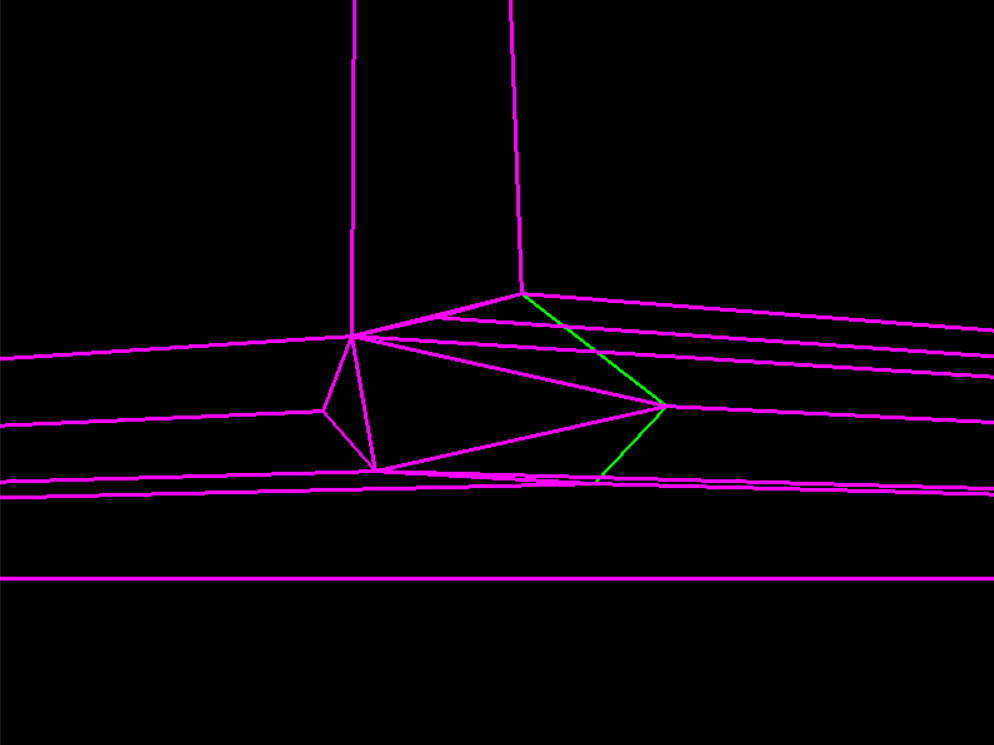 (Обратите внимание, что p0, p1 и p2 выходят за рамки рисунка). Некоторые линии из исходного многоугольника (на этот раз зеленым) до сих пор не добавлены в триангуляцию. Я не уверен, где я иду не так.

Я надеюсь, что код понятен, но я собираюсь объяснить некоторые методы / структуры на всякий случай:

TriPoint

является потомком структуры Point.

p0, p1, p2

три точки образуют ограничивающий треугольник вокруг многоугольника. Я поняла от эта почта.

contains(Point p)

возвращает true, если точка находится в треугольнике или на одном из ребер.

findCommonTriangle(TriPoint *a, TriPoint *b, Triangle *t)

возвращает треугольник, падающий на t вдоль ребра ab. (Я не использую Edges для вычисления триангуляции, поэтому я решил получить треугольник инцидента таким образом).

isOnTriangle(Point s)

вызывается для треугольника abc и возвращает 1, если точка находится на ребре ab, 2, если точка находится на ребре bc, 3, если точка находится на ребре cd. Если он находится в треугольнике, он возвращает 0.

Код для самой триангуляции находится ниже:

    #include <GL\glew.h>
#include <GL\freeglut.h>
#include <iostream>

#include <array>
#include <vector>
#include "predicates.h"
struct Point {
float x, y;
Point() { }
Point(float a, float b) {
x = a;
y = b;
}
};

struct Triangle;
struct Triangulation;
std::vector<Triangulation *> triangulations;

struct TriPoint : Point {
std::vector<Triangle *> triangles;
TriPoint() { };
int index;
TriPoint(Point a) {
x = a.x;
y = a.y;
}
TriPoint(float x, float y) : Point(x, y) {};
void removeTriangle(Triangle *t) {
for (size_t i = 0; i < triangles.size(); i++) {
if (triangles[i] == t) {
triangles.erase(triangles.begin() + i);
}
}
}
void addTriangle(Triangle *t) {
triangles.push_back(t);
}
};

double pointInLine(Point *a, Point *b, Point *p) {
REAL *A, *B, *P;
A = new REAL[2];
B = new REAL[2];
P = new REAL[2];
A[0] = a->x;
A[1] = a->y;
B[0] = b->x;
B[1] = b->y;
P[0] = p->x;
P[1] = p->y;
double orient = orient2d(A, B, P);
delete(A);
delete(B);
delete(P);
return orient;
}

struct Triangle {
TriPoint *a, *b, *c;
std::vector<Triangle *> children;
Triangle() { };
Triangle(TriPoint *x, TriPoint *y, TriPoint *z) {
a = x;
b = y;
c = z;
orientTri();
x->addTriangle(this);
y->addTriangle(this);
z->addTriangle(this);
}
bool hasChildren() {
return children.size() != 0;
}
void draw() {
glBegin(GL_LINE_STRIP);
glVertex2f(a->x, a->y);
glVertex2f(b->x, b->y);
glVertex2f(c->x, c->y);
glVertex2f(a->x, a->y);
glEnd();
}
bool contains(Point s) {
float as_x = s.x - a->x;
float as_y = s.y - a->y;

bool s_ab = (b->x - a->x)*as_y - (b->y - a->y)*as_x > 0;
if ((c->x - a->x)*as_y - (c->y - a->y)*as_x > 0 == s_ab) return false;
if ((c->x - b->x)*(s.y - b->y) - (c->y - b->y)*(s.x - b->x) > 0 != s_ab) return false;
return true;
}
int isOnTriangle(Point p) {
//Return -1 if outside
//Returns 1 if on AB
//Returns 2 if on BC
//Returns 3 if on CA
//Returns 4 if on B
//Returns 5 if on C
//Returns 6 if on A
double res1 = pointInLine(b, a, &p);
double res2 = pointInLine(c, b, &p);
double res3 = pointInLine(a, c, &p);

/*If triangles are counter-clockwise oriented then a point is inside
the triangle if the three 'res' are < 0, at left of each oriented edge
*/
if (res1 > 0 || res2 > 0 || res3 > 0)
return -1; //outside
if (res1 < 0) {
if (res2 < 0) {
if (res3 < 0) {
return 0; //inside
} else { //res3 == 0
return 3; //on edge3
}
} else { //res2 == 0
if (res3 == 0) {
return 5; //is point shared by edge2 and edge3
}
return 2; //on edge2
}
} else { //res1 == 0
if (res2 == 0) {
return 4; //is point shared by edge1 and edge2
} else if (res3 == 0) {
return 6; //is point shared by edge1 and 3
}
return 1; //on edge 1
}
}

TriPoint *getThirdPoint(TriPoint *x, TriPoint *y) {
if (a != x && a != y)
return a;
if (b != x && b != y)
return b;
return c;
}
bool hasPoint(TriPoint *p) {
return a == p || b == p || c == p;
}
void orientTri() {
REAL *A, *B, *C;
A = new REAL[2];
B = new REAL[2];
C = new REAL[2];
A[0] = a->x;
A[1] = a->y;
B[0] = b->x;
B[1] = b->y;
C[0] = c->x;
C[1] = c->y;
double orientation = orient2d(A, B, C);
if (orientation < 0) {
TriPoint *temp = a;
a = b;
b = temp;
}
delete(A);
delete(B);
delete(C);
}
};

struct Poly {
std::vector<Point> points;
bool selected = false;
};Triangle *findCommonTriangle(TriPoint *a, TriPoint *b, Triangle *t) {
//Returns a triangle shared by a and b incident to t
for (Triangle *aTri : a->triangles) {
for (Triangle *bTri : b->triangles) {
if (aTri == bTri && aTri != t) {
return aTri;
}
}
}
return NULL;
}

struct Triangulation {
std::vector<Point> points;
std::vector<Triangle *> triangles;
float xMin = 9999;
float xMax = 0;
float yMin;
float yMax;
Triangulation() { };
Triangulation(Poly p) {
points = p.points;
sort();
triangulate();
}
void draw() {
for (Triangle *t : triangles) {
t->draw();
}
}
void sort() {
//Sort by y-value in ascending order.
//If y-values are equal, sort by x in ascending order.
for (size_t i = 0; i < points.size() - 1; i++) {
if (points[i].x < xMin) {
xMin = points[i].x;
}
if (points[i].x > xMax) {
xMax = points[i].x;
}
int index = i;
for (size_t j = i; j < points.size(); j++) {
if (points[index].y > points[j].y) {
index = j;
} else if (points[index].y == points[j].y) {
if (points[index].x > points[j].x) {
index = j;
}
}
}
std::swap(points[i], points[index]);
}
yMin = points[0].y;
yMax = points[points.size() - 1].y;
std::random_shuffle(points.begin(), points.end());
}
void triangulate() {
Triangle *root;
float dx = xMax - xMin;
float dy = yMax - yMin;
float deltaMax = std::max(dx, dy);
float midx = (xMin + xMax) / 2.f;
float midy = (yMin + yMax) / 2.f;

TriPoint *p0;
TriPoint *p1;
TriPoint *p2;
p0 = new TriPoint(midx - 2 * deltaMax, midy - deltaMax);
p1 = new TriPoint(midx, midy + 2 * deltaMax);
p2 = new TriPoint(midx + 2 * deltaMax, midy - deltaMax);
p0->index = 0;
p1->index = -1;
p2->index = -2;

root = new Triangle(p0, p1, p2);
for (size_t i = 0; i < points.size(); i++) {
TriPoint *p = new TriPoint(points[i]);
p->index = i + 1;
Triangle *temp = root;
double in;
while (temp->hasChildren()) {
for (size_t j = 0; j < temp->children.size(); j++) {
in = temp->children[j]->isOnTriangle(points[i]);
if (in >= 0) {
temp = temp->children[j];
break;
}
}
}

in = temp->isOnTriangle(points[i]);
if (in > 0 ) { //Boundary
if (in == 1) { //AB
Triangle *other = findCommonTriangle(temp->a, temp->b, temp);
TriPoint *l = other->getThirdPoint(temp->a, temp->b);
l->removeTriangle(other);
temp->a->removeTriangle(other);
temp->b->removeTriangle(other);
temp->a->removeTriangle(temp);
temp->b->removeTriangle(temp);
temp->c->removeTriangle(temp);
Triangle *n1 = new Triangle(temp->a, p, temp->c);
Triangle *n2 = new Triangle(temp->b, temp->c, p);
Triangle *n3 = new Triangle(temp->a, l, p);
Triangle *n4 = new Triangle(temp->b, p, l);

temp->children.push_back(n1);
temp->children.push_back(n2);
other->children.push_back(n3);
other->children.push_back(n4);
} else if (in == 2) { //BC
Triangle *other = findCommonTriangle(temp->b, temp->c, temp);
TriPoint *l = other->getThirdPoint(temp->b, temp->c);
l->removeTriangle(other);
temp->b->removeTriangle(other);
temp->c->removeTriangle(other);
temp->a->removeTriangle(temp);
temp->b->removeTriangle(temp);
temp->c->removeTriangle(temp);
Triangle *n1 = new Triangle(temp->a, p, temp->c);
Triangle *n2 = new Triangle(temp->b, temp->a, p);
Triangle *n3 = new Triangle(temp->c, p, l);
Triangle *n4 = new Triangle(temp->b, l, p);

temp->children.push_back(n1);
temp->children.push_back(n2);
other->children.push_back(n3);
other->children.push_back(n4);
} else if (in == 3) { //CA
Triangle *other = findCommonTriangle(temp->a, temp->c, temp);
TriPoint *l = other->getThirdPoint(temp->a, temp->c);
l->removeTriangle(other);
temp->a->removeTriangle(other);
temp->c->removeTriangle(other);
temp->a->removeTriangle(temp);
temp->b->removeTriangle(temp);
temp->c->removeTriangle(temp);

Triangle *n1 = new Triangle(temp->b, temp->c, p);
Triangle *n2 = new Triangle(temp->a, temp->b, p);
Triangle *n3 = new Triangle(temp->c, l, p);
Triangle *n4 = new Triangle(temp->a, p, l);

temp->children.push_back(n1);
temp->children.push_back(n2);
other->children.push_back(n3);
other->children.push_back(n4);
}
} else { //Point is inside of triangle
Triangle *t1 = new Triangle(temp->a, temp->b, p);
Triangle *t2 = new Triangle(temp->b, temp->c, p);
Triangle *t3 = new Triangle(temp->c, temp->a, p);

temp->a->removeTriangle(temp);
temp->b->removeTriangle(temp);
temp->c->removeTriangle(temp);

temp->children.push_back(t1);
temp->children.push_back(t2);
temp->children.push_back(t3);
}
} //Triangulation done
findSmallest(root, p0, p1, p2);
triangulations.push_back(this);
}

void findSmallest(Triangle *root, TriPoint *p0, TriPoint *p1, TriPoint *p2) {
bool include = true; //Controls drawing triangles with p0, p1, and p2
if (root->hasChildren()) {
for (Triangle *t : root->children) {
findSmallest(t, p0, p1, p2);
}
} else {
int i0 = root->hasPoint(p0);
int i1 = root->hasPoint(p1);
int i2 = root->hasPoint(p2);
if ((!i0 && !i1 && !i2) || include) {
triangles.push_back(root);
}
}
}
};

Poly polygon;

void changeViewPort(int w, int h)
{
glViewport(0, 0, w, h);
glMatrixMode(GL_PROJECTION);
glLoadIdentity();
glOrtho(0, glutGet(GLUT_WINDOW_WIDTH), 0, glutGet(GLUT_WINDOW_HEIGHT), -1, 1);
glMatrixMode(GL_MODELVIEW);
glLoadIdentity();
glTranslatef(0.375, 0.375, 0.0);
}

void render() {
glClear(GL_COLOR_BUFFER_BIT);
glLineWidth(2.5);
changeViewPort(glutGet(GLUT_WINDOW_WIDTH), glutGet(GLUT_WINDOW_HEIGHT));

glColor3f(0, 0, 1); //Blue
glBegin(GL_LINE_STRIP);
for (size_t j = 0; j < polygon.points.size(); j++) {
std::vector<Point> ps = polygon.points;
Point p1 = ps[j];
glVertex2i(p1.x, p1.y);
}
glVertex2i(polygon.points[0].x, polygon.points[0].y);
glEnd();

glColor3f(1, 0, 1);
for (Triangulation *t : triangulations) {
t->draw();
}

glutSwapBuffers();
}

int main(int argc, char* argv[]) {
glutInit(&argc, argv);
glutInitDisplayMode(GLUT_DOUBLE | GLUT_RGBA | GLUT_DEPTH);
glutInitWindowSize(800, 600);
glutCreateWindow("Stack Overflow Question");
glutReshapeFunc(changeViewPort);
glutDisplayFunc(render);

exactinit();

polygon.points.push_back(*new Point(300.0f, 300.0f));
polygon.points.push_back(*new Point(300.0f, 400.0f));
polygon.points.push_back(*new Point(400.0f, 400.0f));
polygon.points.push_back(*new Point(400.0f, 300.0f));
Triangulation t = *(new Triangulation(polygon));

glutMainLoop();
return 0;
}

Примечание: предикаты и предикаты были созданы с использованием кода из Вот.