Округление трехмерной точки относительно плоскости
У меня есть класс самолета, который содержит N для нормального и Q для точки на плоскости. У меня тоже есть еще один момент п это также лежит на этом плане. Как мне идти о округлении п до ближайшего подразделения на этой плоскости. Как привязка курсора к трехмерной сетке, но сетка может вращаться в плоскости.
Изображение, чтобы объяснить: 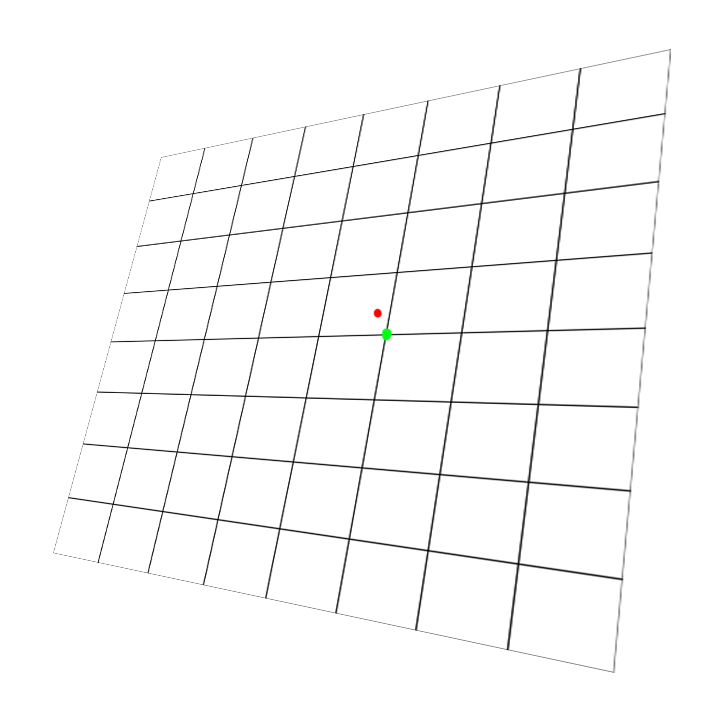
Красный — текущая точка. Зеленый — это округленная точка, которую я пытаюсь получить.
Решение
Вероятно, самый простой способ добиться этого — взять плоскость для определения повернутой и сдвинутой системы координат. Это позволяет построить матрицы для преобразования точки в глобальных координатах в координаты плоскости и обратно. Получив это, вы можете просто преобразовать точку в координаты плоскости, выполнить округление / проекцию тривиальным образом и преобразовать обратно в мировые координаты.
Конечно, проблема недостаточно конкретизирована в том, как вы задаете вопрос: нужное преобразование имеет шесть степеней свободы, а ваше плоское уравнение дает только три ограничения. Таким образом, вам нужно добавить еще немного информации: местоположение начала координат в плоскости и вращение вашей сетки вокруг плоскости нормали.
Лично я бы начал с описания плоскости в параметрической форме:
xVec = alpha*direction1 + beta*direction2 + x0
Конечно, такое описание содержит девять переменных (три вектора), но вы можете нормализовать два вектора направления, и вы можете ограничить два вектора направления ортогональностью, что уменьшает количество свобод до шести.
Два нормализованных вектора направления вместе с нормализованной нормалью являются базовыми векторами повернутой системы координат, поэтому вы можете просто построить матрицу вращения, сложив эти три вектора вместе. Чтобы получить обратное вращение, просто транспонируйте полученную матрицу. Добавьте перевод / обратный перевод на соответствующую сторону вращения, и все готово.
Другие решения
Других решений пока нет …
