Очень быстрая сортировка массивов фиксированной длины с использованием компараторных сетей
У меня есть некоторый критичный к производительности код, который включает в себя сортировку очень короткого массива фиксированной длины с примерно 3-10 элементами в C ++ (параметр изменяется во время компиляции).
Мне пришло в голову, что статическая сеть сортировки, специализированная для каждого возможного размера ввода, возможно, будет очень эффективным способом сделать это: мы делаем все сравнения, необходимые, чтобы выяснить, в каком случае мы находимся, затем делаем оптимальное количество перестановок для сортировки массив.
Чтобы применить это, мы используем немного магии шаблона, чтобы определить длину массива и применить правильную сеть:
#include <iostream>
using namespace std;
template< int K >
void static_sort(const double(&array)[K])
{
cout << "General static sort\n" << endl;
}
template<>
void static_sort<3>(const double(&array)[3])
{
cout << "Static sort for K=3" << endl;
}int main()
{
double array[3];
// performance critical code.
// ...
static_sort(array);
// ...
}
Очевидно, что это все сложнее, так что:
- У кого-нибудь есть мнение о том, стоит ли это усилий?
- Кто-нибудь знает, существует ли эта оптимизация в каких-либо стандартных реализациях, например, std :: sort?
- Есть ли простое место, чтобы получить код, реализующий такую сортировочную сеть?
- Возможно, было бы возможно создать сеть сортировки, подобную этой, статически, используя шаблонную магию.
Пока я просто использую сортировку вставкой со статическим параметром шаблона (как выше), в надежде, что это будет способствовать развертыванию и другим оптимизациям во время компиляции.
Ваши мысли приветствуются.
Обновить:
Я написал тестовый код для сравнения «статической» вставки short и std :: sort. (Когда я говорю «статический», я имею в виду, что размер массива фиксирован и выводится во время компиляции (предположительно, с возможностью развертывания цикла и т. Д.).
Я получаю как минимум 20% -ное улучшение NET (обратите внимание, что генерация включена в сроки). Платформа: clang, OS X 10.9.
Код здесь https://github.com/rosshemsley/static_sorting если вы хотите сравнить его с вашими реализациями stdlib.
Мне еще предстоит найти хороший набор реализаций для сортировщиков сетей компараторов.
Решение
Недавно я написал небольшой класс, который использует алгоритм Бозе-Нельсона для генерации сети сортировки во время компиляции.
/**
* A Functor class to create a sort for fixed sized arrays/containers with a
* compile time generated Bose-Nelson sorting network.
* \tparam NumElements The number of elements in the array or container to sort.
* \tparam T The element type.
* \tparam Compare A comparator functor class that returns true if lhs < rhs.
*/
template <unsigned NumElements, class Compare = void> class StaticSort
{
template <class A, class C> struct Swap
{
template <class T> inline void s(T &v0, T &v1)
{
T t = Compare()(v0, v1) ? v0 : v1; // Min
v1 = Compare()(v0, v1) ? v1 : v0; // Max
v0 = t;
}
inline Swap(A &a, const int &i0, const int &i1) { s(a[i0], a[i1]); }
};
template <class A> struct Swap <A, void>
{
template <class T> inline void s(T &v0, T &v1)
{
// Explicitly code out the Min and Max to nudge the compiler
// to generate branchless code.
T t = v0 < v1 ? v0 : v1; // Min
v1 = v0 < v1 ? v1 : v0; // Max
v0 = t;
}
inline Swap(A &a, const int &i0, const int &i1) { s(a[i0], a[i1]); }
};
template <class A, class C, int I, int J, int X, int Y> struct PB
{
inline PB(A &a)
{
enum { L = X >> 1, M = (X & 1 ? Y : Y + 1) >> 1, IAddL = I + L, XSubL = X - L };
PB<A, C, I, J, L, M> p0(a);
PB<A, C, IAddL, J + M, XSubL, Y - M> p1(a);
PB<A, C, IAddL, J, XSubL, M> p2(a);
}
};
template <class A, class C, int I, int J> struct PB <A, C, I, J, 1, 1>
{
inline PB(A &a) { Swap<A, C> s(a, I - 1, J - 1); }
};
template <class A, class C, int I, int J> struct PB <A, C, I, J, 1, 2>
{
inline PB(A &a) { Swap<A, C> s0(a, I - 1, J); Swap<A, C> s1(a, I - 1, J - 1); }
};
template <class A, class C, int I, int J> struct PB <A, C, I, J, 2, 1>
{
inline PB(A &a) { Swap<A, C> s0(a, I - 1, J - 1); Swap<A, C> s1(a, I, J - 1); }
};
template <class A, class C, int I, int M, bool Stop = false> struct PS
{
inline PS(A &a)
{
enum { L = M >> 1, IAddL = I + L, MSubL = M - L};
PS<A, C, I, L, (L <= 1)> ps0(a);
PS<A, C, IAddL, MSubL, (MSubL <= 1)> ps1(a);
PB<A, C, I, IAddL, L, MSubL> pb(a);
}
};
template <class A, class C, int I, int M> struct PS <A, C, I, M, true>
{
inline PS(A &a) {}
};
public:
/**
* Sorts the array/container arr.
* \param arr The array/container to be sorted.
*/
template <class Container> inline void operator() (Container &arr) const
{
PS<Container, Compare, 1, NumElements, (NumElements <= 1)> ps(arr);
};
/**
* Sorts the array arr.
* \param arr The array to be sorted.
*/
template <class T> inline void operator() (T *arr) const
{
PS<T*, Compare, 1, NumElements, (NumElements <= 1)> ps(arr);
};
};
#include <iostream>
#include <vector>
int main(int argc, const char * argv[])
{
enum { NumValues = 32 };
// Arrays
{
int rands[NumValues];
for (int i = 0; i < NumValues; ++i) rands[i] = rand() % 100;
std::cout << "Before Sort: \t";
for (int i = 0; i < NumValues; ++i) std::cout << rands[i] << " ";
std::cout << "\n";
StaticSort<NumValues> staticSort;
staticSort(rands);
std::cout << "After Sort: \t";
for (int i = 0; i < NumValues; ++i) std::cout << rands[i] << " ";
std::cout << "\n";
}
std::cout << "\n";
// STL Vector
{
std::vector<int> rands(NumValues);
for (int i = 0; i < NumValues; ++i) rands[i] = rand() % 100;
std::cout << "Before Sort: \t";
for (int i = 0; i < NumValues; ++i) std::cout << rands[i] << " ";
std::cout << "\n";
StaticSort<NumValues> staticSort;
staticSort(rands);
std::cout << "After Sort: \t";
for (int i = 0; i < NumValues; ++i) std::cout << rands[i] << " ";
std::cout << "\n";
}
return 0;
}
Ориентиры
Следующие тесты скомпилированы с помощью clang -O3 и запущены на моем MacBook Air в середине 2012 года.
Время (в миллисекундах) для сортировки 1 миллиона массивов.
Количество миллисекунд для массивов размером 2, 4, 8 составляет 1,943, 8,655 и 20,246 соответственно.
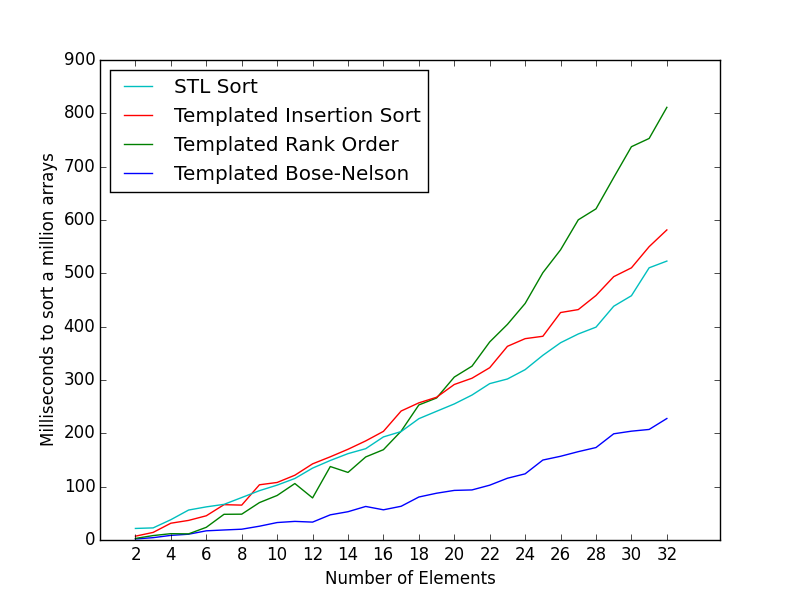
Вот средние часы на сортировку для маленьких массивов из 6 элементов. Код теста и примеры можно найти по этому вопросу:
Самый быстрый вид массива с фиксированной длиной 6 int
Direct call to qsort library function : 342.26
Naive implementation (insertion sort) : 136.76
Insertion Sort (Daniel Stutzbach) : 101.37
Insertion Sort Unrolled : 110.27
Rank Order : 90.88
Rank Order with registers : 90.29
Sorting Networks (Daniel Stutzbach) : 93.66
Sorting Networks (Paul R) : 31.54
Sorting Networks 12 with Fast Swap : 32.06
Sorting Networks 12 reordered Swap : 29.74
Reordered Sorting Network w/ fast swap : 25.28
Templated Sorting Network (this class) : 25.01
Он работает так же быстро, как самый быстрый пример в вопросе для 6 элементов.
Код, используемый для тестов можно найти Вот.
Другие решения
Другие ответы интересны и довольно хороши, но я считаю, что могу предоставить некоторые дополнительные элементы ответа, пункт за пункт:
- Стоит ли усилий? Что ж, если вам нужно отсортировать небольшие коллекции целых чисел, а сети сортировки настроены так, чтобы максимально использовать некоторые инструкции, это может стоить усилий. На следующем графике представлены результаты сортировки миллиона массивов
intразмером 0-14 с различными алгоритмами сортировки. Как вы можете видеть, сети сортировки могут обеспечить значительное ускорение, если вам это действительно нужно.
-
Нет стандартной реализации
std::sortЯ знаю об использовании сортировочных сетей; когда они не настроены точно, они могут быть медленнее, чем прямой тип вставки. Libc ++ sstd::sortимеет специальные алгоритмы для сортировки от 0 до 5 значений одновременно, но они также не используют сети сортировки. Единственный известный мне алгоритм сортировки, который использует сортировочные сети для сортировки нескольких значений: Wikisort. Тем не менее, исследовательская работа Применение сетей сортировки для синтеза оптимизированных библиотек сортировки предполагает, что сети сортировки могут использоваться для сортировки небольших массивов или для улучшения алгоритмов рекурсивной сортировки, таких как быстрая сортировка, но только в том случае, если они настроены так, чтобы использовать преимущества конкретных аппаратных инструкций.доступ выравнивается сортировка Алгоритм — это своего рода восходящая сортировка, которая, по-видимому, использует сети с битовой сортировкой, реализованные с инструкциями SIMD для первого прохода. По-видимому, алгоритм может быть быстрее стандартной библиотеки для некоторых скалярных типов.
-
Я действительно могу предоставить такую информацию по той простой причине, что я разработал библиотека сортировки C ++ 14 это обеспечивает эффективные сети сортировки размером от 0 до 32, которые реализуют оптимизации, описанные в предыдущем разделе. Я использовал его для генерации графика в первом разделе. Я все еще работаю над частью библиотеки для сортировочных сетей, чтобы обеспечить оптимальные по размеру, оптимальным по глубине и оптимальным по размерам сети. Небольшие оптимальные сети сортировки обнаруживаются с помощью грубой силы, в то время как большие сети сортировки используют результаты литературы.
Обратите внимание, что ни один из алгоритмов сортировки в библиотеке не использует сети сортировки напрямую, но вы можете адаптировать их так, чтобы сеть сортировки выбиралась всякий раз, когда алгоритму сортировки дается небольшой
std::arrayили небольшой массив C фиксированного размера:using namespace cppsort; // Sorters are function objects that can be // adapted with sorter adapters from the // library using sorter = small_array_adapter< std_sorter, sorting_network_sorter >; // Now you can use it as a function sorter sort; // Instead of a size-agnostic sorting algorithm, // sort will use an optimal sorting network for // 5 inputs since the bound of the array can be // deduced at compile time int arr[] = { 2, 4, 7, 9, 3 }; sort(arr);Как упоминалось выше, библиотека предоставляет эффективные сети сортировки для встроенных целых чисел, но вам, вероятно, не повезет, если вам нужно отсортировать небольшие массивы чего-то еще (например мои последние тесты показывают, что они не лучше, чем прямая вставка сортировки даже для
long long int). -
Возможно, вы могли бы использовать шаблонное метапрограммирование для генерации сетей сортировки любого размера, но ни один из известных алгоритмов не может создать лучшие сети сортировки, поэтому вы могли бы также написать лучшие вручную. Я не думаю, что те, которые генерируются простыми алгоритмами, могут в любом случае обеспечить полезные и эффективные сети (единственно используемые сети с нечетно-четной сортировкой и попарной сортировкой Бэтчера могут быть) [Другой ответ, кажется, показывает, что сгенерированные сети действительно могут работать].
Известны оптимальные или, по крайней мере, лучшие сети компараторов длины для N<16, так что, по крайней мере, есть неплохая отправная точка. Справедливо, поскольку оптимальные сети не обязательно рассчитаны на максимальный уровень параллелизм достижимо, например, с помощью SSE или другая векторная арифметика.
Другое дело, что уже некоторые оптимальные сети для некоторого N являются вырожденными версиями для немного большей оптимальной сети для N + 1.
От википедия:
Оптимальные глубины до 10 входов известны, и они
соответственно 0, 1, 3, 3, 5, 5, 6, 6, 7, 7.
Тем не менее, я буду стремиться к реализации сетей для N = {4, 6, 8 и 10}, так как ограничение глубины не может быть смоделировано дополнительным параллелизмом (я думаю). Я также думаю, что способность работать в регистрах SSE (также с использованием некоторых инструкций min / max) или даже относительно большого набора регистров в архитектуре RISC обеспечит заметное преимущество в производительности по сравнению с «хорошо известными» методами сортировки, такими как быстрая сортировка, из-за отсутствие арифметики указателя и других накладных расходов.
Кроме того, я стремлюсь реализовать параллельную сеть, используя трюк с печально известной петлей Устройство Даффа.
РЕДАКТИРОВАТЬ
Когда известно, что входные значения являются положительными значениями IEEE-754 с плавающей точкой или двойными числами, также стоит упомянуть, что сравнение также может быть выполнено как целые числа. (float и int должны иметь одинаковые порядковые номера)
Позвольте мне поделиться некоторыми мыслями.
Есть ли у кого-нибудь мнение о том, стоит ли это
усилия?
Невозможно дать правильный ответ. Вы должны профилировать свой фактический код, чтобы узнать это.
В моей практике, когда дело доходит до низкоуровневого профилирования, узкое место всегда было не там, где я думал.
Кто-нибудь знает, существует ли эта оптимизация в каком-либо стандарте?
реализации, например, std :: sort?
Например, реализация Visual C ++ std::sort использует сортировку вставки для маленьких векторов. Я не знаю о реализации, которая использует оптимальные сети сортировки.
Возможно, можно было бы создать такую сортировочную сеть, как эта
статически используя шаблон магии
Существуют алгоритмы генерации сортировочных сетей, такие как алгоритмы Бозе-Нельсона, Хиббарда и Бэтчера. Поскольку шаблоны C ++ полны по Тьюрингу, вы можете реализовать их с помощью TMP. Однако эти алгоритмы не гарантируют теоретически минимальное количество компараторов, поэтому вы можете захотеть жестко закодировать оптимальную сеть.
