Оценщик плотности ядра (с ядром Гаусса) Sum f (x) = 1?

Question

Оценщик плотности ядра (с ядром Гаусса) Sum f (x) = 1?

Я хочу использовать KDE с Гауссово ядро. Если я прав, сумма всех f (x) должна быть 1 (округление)?

Моя реализация выглядит так:

    float K( float const& val)
{
const float p=1.0 / std::sqrt( 2.0 * M_PI);
float result = 0.5 * (val*val);
result = p * std::exp(- result);

return result;
};

std::vector< std::pair<float, float> kde( float *val, int len float h)
{
std::vector< std::pair<float, float>> density( len );
const float p = 1.0 / (h * len );

for(int r=0;r<len;r++)
{
float sum = 0;

for(int i=0;i<len;i++)
sum += k( (val[r] - val[i]) / h );

density[r] = std::make_pair( val[r], p*sum );
}
return density;
}

И я выбрал h> 0. Я прав, что р * сумма вероятность для значения Val [г] ? Сумма по всей вероятности> 1 (но выглядит хорошо для меня).

2

c++gaussian kernel-density probability-density

Решение

Другие решения

Источник

Accepted Answer

Вы неверно истолковали предположения о плотности вероятности здесь. Плотность интегрирует к одному, тогда как его значения в определенных точках определенно не 1.

Давайте обсудим это, используя следующую формулу из связанная статья в Википедии который вы, кажется, используете:

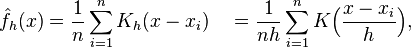
введите описание изображения здесь

Эта формула обеспечивает плотность f_h(x) оценивается в точке x,

Из моего обзора ваш код правильно оценивает это количество. Тем не менее, вы неверно истолковали количество, которое должно быть единица. Как плотность, интеграл по всему пространству должен дать один, т.е.

$\ large \ int f_h (x) \, dx \ = \ 1$

Это свойство называется нормализация плотности.

Более того, будучи самой плотностью, каждое слагаемое f_h(x) должен уступить 1/n при интегрировании по всему пространству, когда также включается константа нормализации. Опять же, нет гарантии на значения слагаемых.

В одном измерении вы можете легко подтвердить нормализацию, используя правило трапеции или другую квадратурную схему (- если вы предоставите рабочий пример, я могу попытаться это сделать).

2