Обнаружение столкновения между 2 «линейно» движущиеся объекты в WGS84

[Edit5] Завершите reedit, если вам нужны старые источники, смотрите историю изменений

Как отметил Нико Шертлер, проверка пересечения между линиями — это безумие, так как вероятность пересечения двух траекторий в одном и том же положении и времени практически отсутствует (даже с учетом совпадений точности округления). Вместо этого вы должны найти место на каждой траектории, которое достаточно близко (чтобы столкнуться), и оба объекта находятся там относительно одновременно. Другая проблема заключается в том, что ваши траектории не являются линейными вообще. Да, они могут казаться линейными для коротких времен в кабине WGS84 и декартовой, но с увеличением времени траектория изгибается вокруг Земли. Кроме того, ваши единицы входных значений для скорости делают это немного сложнее, поэтому позвольте мне повторить нормализованные значения, с которыми я сейчас буду иметь дело:

1. вход

   состоит из двух объектов. Для каждого известна его фактическая позиция (в WGS84 [rad]) и фактические скорости [m/s] но не в декартовом пространстве, а WGS84 локальные оси вместо. Например что-то вроде этого:

   const double kmh=1.0/3.6;
   const double deg=M_PI/180.0;
   const double rad=180.0/M_PI;
   //                      lon            lat      alt
   double pos0[3]={  23.000000*deg, 48.000000*deg,2500.000000 };
   double pos1[3]={  23.000000*deg, 35.000000*deg,2500.000000 };
   double vel0[3]={ 100.000000*kmh,-20.000000*kmh,   0.000000*kmh };
   double vel1[3]={ 100.000000*kmh, 20.000000*kmh,   0.000000*kmh };
   

   Осторожно, мои координаты находятся в Long,Lat,Alt порядок / соглашение !!!

2. выход

   Вам необходимо вычислить время, в которое два объекта «сталкиваются». Дополнительные ограничения к решению могут быть добавлены позднее. Как упоминалось ранее, мы ищем не пересечение, а «самый близкий» подход, который удовлетворяет условиям столкновения (например, расстояние меньше некоторого порога).

После некоторого обучения и тестирования я решил использовать итеративный подход в WGS84 пространство. Это поднимает некоторые проблемы, например, как конвертировать скорость в [m/s] в WGS84 пространство для [rad/s] в WGS84 пространство. Это соотношение меняется в зависимости от высоты объекта и широты. На самом деле нам нужно вычислить изменение угла в long а также lat оси, которые «точно» равны 1m пройденное расстояние, а затем умножьте скорости на него. Это может быть аппроксимировано уравнением длины дуги:

l = dang.R

куда R фактический радиус углового перемещения, ang это изменение угла и l пройденное расстояние, поэтому, когда l=1.0 затем:

dang = 1.0/R

Если у нас есть декартова позиция x,y,z (z является осью вращения Земли) тогда:

Rlon = sqrt (x*x + y*y)
Rlat = sqrt (x*x + y*y + z*z)

Теперь мы можем перебирать позиции со временем, которые можно использовать для аппроксимации времени ближайшего сближения. Однако нам нужно ограничить максимальный шаг по времени, чтобы мы не пропускали большую часть кривизны Земли. Этот предел зависит от используемых скоростей и точности цели. Итак, вот алгоритм, чтобы найти подход:

1. в этом

   установить начальный шаг времени к верхнему пределу, как dt=1000.0 и вычислить фактическое положение объектов стенда в декартовом пространстве. Из этого вычислить их расстояние d1,

2. итерация

   задавать d0=d1 затем вычислите фактические скорости в WGS84 для фактических позиций и добавить speed*dt каждому объекту актуально WGS84 позиция. Теперь просто вычислите фактические позиции в декартовом пространстве и вычислите их расстояние d1

   если d0>d1 затем мы приближаемся к ближайшему подходу, так что # 2 снова.
   
   В случае d0==d1 траектории параллельны, поэтому время возврата t=0.0
   
   В случае d0<d1 мы уже перешли самый близкий подход, так что установите dt = -0.1*dt и если dt>=desired_accuracy идти к # 2 иначе остановись.

3. восстановить лучше t

   После итерации в # 2 мы должны восстановить лучшее время назад, чтобы вернуться t+10.0*dt;

Теперь у нас самое близкое время приближения t, Остерегайтесь, это может быть отрицательным (если объекты удаляются друг от друга). Теперь вы можете добавить свои ограничения как

if (d0<_max_d)
if ((t>=0.0)&&(t<=_max_T))
return collision ...

Вот C ++ Источник для этого:

//---------------------------------------------------------------------------
#include <math.h>
//---------------------------------------------------------------------------
const double kmh=1.0/3.6;
const double deg=M_PI/180.0;
const double rad=180.0/M_PI;
const double  _earth_a=6378137.00000;   // [m] WGS84 equator radius
const double  _earth_b=6356752.31414;   // [m] WGS84 epolar radius
const double  _earth_e=8.1819190842622e-2; //  WGS84 eccentricity
const double  _earth_ee=_earth_e*_earth_e;
//--------------------------------------------------------------------------
const double _max_d=2500.0;         // [m] collision gap
const double _max_T=3600000.0;      // [s] max collision time
const double _max_dt=1000.0;        // [s] max iteration time step (for preserving accuracy)
//--------------------------------------------------------------------------
//                      lon            lat      alt
double pos0[3]={  23.000000*deg, 48.000000*deg,2500.000000 }; // [rad,rad,m]
double pos1[3]={  23.000000*deg, 35.000000*deg,2500.000000 }; // [rad,rad,m]
double vel0[3]={ 100.000000*kmh,-20.000000*kmh,   0.000000*kmh }; // [m/s,m/s,m/s]
double vel1[3]={ 100.000000*kmh,+20.000000*kmh,   0.000000*kmh }; // [m/s,m/s,m/s]
//---------------------------------------------------------------------------
double divide(double x,double y)
{
if ((y>=-1e-30)&&(y<=+1e-30)) return 0.0;
return x/y;
}
void  vector_copy(double *c,double *a)         { for(int i=0;i<3;i++) c[i]=a[i];       }
double vector_len(double *a) { return sqrt((a[0]*a[0])+(a[1]*a[1])+(a[2]*a[2])); }
void  vector_len(double *c,double *a,double l)
{
l=divide(l,sqrt((a[0]*a[0])+(a[1]*a[1])+(a[2]*a[2])));
c[0]=a[0]*l;
c[1]=a[1]*l;
c[2]=a[2]*l;
}
void  vector_sub(double *c,double *a,double *b) { for(int i=0;i<3;i++) c[i]=a[i]-b[i]; }
//---------------------------------------------------------------------------
void WGS84toXYZ(double *xyz,double *abh)
{
double  a,b,h,l,c,s;
a=abh[0];
b=abh[1];
h=abh[2];
c=cos(b);
s=sin(b);
// WGS84 from eccentricity
l=_earth_a/sqrt(1.0-(_earth_ee*s*s));
xyz[0]=(l+h)*c*cos(a);
xyz[1]=(l+h)*c*sin(a);
xyz[2]=(((1.0-_earth_ee)*l)+h)*s;
}
//---------------------------------------------------------------------------
void WGS84_m2rad(double &da,double &db,double *abh)
{
// WGS84 from eccentricity
double p[3],rr;
WGS84toXYZ(p,abh);
rr=(p[0]*p[0])+(p[1]*p[1]);
da=divide(1.0,sqrt(rr));
rr+=p[2]*p[2];
db=divide(1.0,sqrt(rr));
}
//---------------------------------------------------------------------------
double collision(double *pos0,double *vel0,double *pos1,double *vel1)
{
int e,i,n;
double p0[3],p1[3],q0[3],q1[3],da,db,dt,t,d0,d1,x,y,z;
vector_copy(p0,pos0);
vector_copy(p1,pos1);
// find closest d1[m] approach in time t[sec]
dt=_max_dt; // [sec] initial time step (accuracy = dt/10^(n-1)
n=6;        // acuracy loops
for (t=0.0,i=0;i<n;i++)
for (e=0;;e=1)
{
d0=d1;
// compute xyz distance
WGS84toXYZ(q0,p0);
WGS84toXYZ(q1,p1);
vector_sub(q0,q0,q1);
d1=vector_len(q0);
// nearest approach crossed?
if (e)
{
if (d0<d1){ dt*=-0.1; break; }                  // crossing trajectories
if (fabs(d0-d1)<=1e-10) { i=n; t=0.0; break; }  // parallel trajectories
}
// apply time step
t+=dt;
WGS84_m2rad(da,db,p0);
p0[0]+=vel0[0]*dt*da;
p0[1]+=vel0[1]*dt*db;
p0[2]+=vel0[2]*dt;
WGS84_m2rad(da,db,p1);
p1[0]+=vel1[0]*dt*da;
p1[1]+=vel1[1]*dt*db;
p1[2]+=vel1[2]*dt;
}
t+=10.0*dt; // recover original t
//  if ((d0<_max_d)&&(t>=0.0)&&(t<=_max_T)) return collision; else return no_collision;
return t;
}
//---------------------------------------------------------------------------

Вот краткий обзор примера:

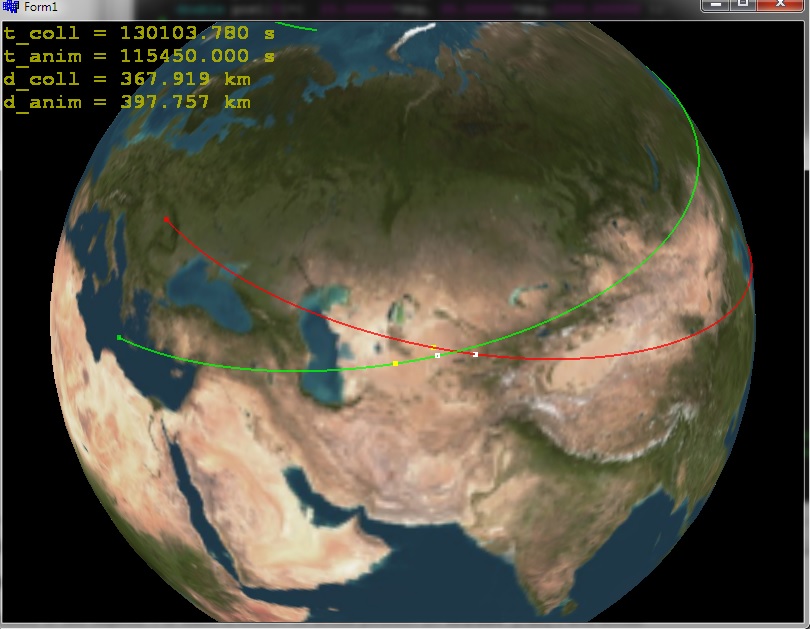
Красный — это объект0, а зеленый — это объект1. Белые квадраты представляют положение при вычисленном столкновении во время t_coll [s] с расстояния d_coll [m], Желтые квадраты — это позиции в определенное пользователем время. t_anim [s] с расстояния d_anim [m] который контролируется пользователем в целях отладки. Как вы можете видеть, этот подход работает также в течение 36 часов …

Надеюсь, я не забыл скопировать что-то (если да, прокомментируйте меня, и я добавлю это)