обнаружение формы дуги и окружности в векторном массиве с диапазоном
У меня есть массив 2d вершин, и я хочу определить, есть ли в массиве какие-либо формы арок или окружностей. Иногда значения не настолько точны, и мне нужен небольшой диапазон. Вот значения. Значение 3-й вертикали остается равным 0:
verticle: -0.014848, -13.2684, 0 angle : 0.141274
verticle: -0.0174556, -4.84519, 0 angle : 90
verticle: 0, 0, 0 angle : 90
verticle: -9.53674e-07, 14.14, 0 angle : 40.7168
verticle: -12.1101, 14.0709, 0 angle : 7.94458
verticle: -12.0996, 10.6442, 0 angle : 0.294751
verticle: -12.2305, 10.6484, 0 angle : 0.24309
verticle: -12.325, 10.6384, 0 angle : 0.349426
verticle: -12.4475, 10.6125, 0 angle : 0.392669
verticle: -12.5638, 10.564, 0 angle : 0.404935
verticle: -12.678, 10.508, 0 angle : 0.34605
verticle: -12.7579, 10.4453, 0 angle : 0.391671
verticle: -12.8315, 10.36, 0 angle : 0.390671
verticle: -12.9051, 10.2747, 0 angle : 0.438795
verticle: -12.9725, 10.1668, 0 angle : 0.455425
verticle: -13.0377, 10.0514, 0 angle : 0.300014
verticle: -13.0407, 9.94522, 0 angle : 0.388662
verticle: -13.0738, 9.83064, 0 angle : 0.338041
verticle: -13.0725, 9.70936, 0 angle : 0.254878
verticle: -13.0412, 9.59645, 0 angle : 0.257171
verticle: -13.0098, 9.48352, 0 angle : 0.259443
verticle: -12.9785, 9.37061, 0 angle : 0.158259
verticle: -12.9192, 9.27357, 0 angle : 0.0713262
verticle: -12.8297, 9.18489, 0 angle : 0.14537
verticle: -12.7724, 9.09539, 0 angle : 0.0484566
verticle: -12.657, 9.03012, 0 angle : 0.0197823
verticle: -12.5738, 8.96403, 0 angle : 0.125115
verticle: -12.4667, 8.92887, 0 angle : 0.219397
verticle: -12.3296, 8.90207, 0 angle : 0.185575
verticle: -12.2288, 8.88951, 0 angle : 0.299361
verticle: -12.1, 8.89282, 0 angle : 11.3066
verticle: -12.1075, 5.64764, 0 angle : 0.158259
verticle: -12.2062, 5.65268, 0 angle : 0.266879
verticle: -12.3329, 5.64184, 0 angle : 0.312787
verticle: -12.4554, 5.61594, 0 angle : 0.384104
verticle: -12.5717, 5.56746, 0 angle : 0.322034
verticle: -12.6557, 5.5198, 0 angle : 0.45024
verticle: -12.7657, 5.44874, 0 angle : 0.416371
verticle: -12.8415, 5.37097, 0 angle : 0.464781
verticle: -12.913, 5.27815, 0 angle : 0.514343
verticle: -12.9803, 5.17027, 0 angle : 0.436111
verticle: -13.0176, 5.07075, 0 angle : 0.487788
verticle: -13.0506, 4.95617, 0 angle : 0.439686
verticle: -13.0515, 4.84242, 0 angle : 0.441462
verticle: -13.0524, 4.72867, 0 angle : 0.470222
verticle: -13.0511, 4.6074, 0 angle : 0.399585
verticle: -13.0198, 4.49448, 0 angle : 0.402998
verticle: -12.9885, 4.38156, 0 angle : 0.305828
verticle: -12.9291, 4.28452, 0 angle : 0.237388
verticle: -12.8396, 4.19585, 0 angle : 0.213062
verticle: -12.7523, 4.1147, 0 angle : 0.188712
verticle: -12.667, 4.04107, 0 angle : 0.0625573
verticle: -12.5557, 3.99086, 0 angle : 0.0279765
verticle: -12.4466, 3.94818, 0 angle : 0.0197823
verticle: -12.3416, 3.92056, 0 angle : 0.158259
verticle: -12.2107, 3.91634, 0 angle : 0.111906
verticle: -12.1121, 3.9113, 0 angle : 17.8633
verticle: -12.0988, 0.00704384, 0 angle : 15.2939
verticle: -12.0895, -3.29836, 0 angle : 0.174713
verticle: -12.2204, -3.29415, 0 angle : 0.100871
verticle: -12.3471, -3.30499, 0 angle : 0.034264
verticle: -12.4395, -3.32253, 0 angle : 0.0395647
verticle: -12.5579, -3.36349, 0 angle : 0.139882
verticle: -12.67, -3.42703, 0 angle : 0.170174
verticle: -12.7499, -3.48974, 0 angle : 0.236563
verticle: -12.8557, -3.57586, 0 angle : 0.266144
verticle: -12.9293, -3.66115, 0 angle : 0.363156
verticle: -12.9666, -3.76067, 0 angle : 0.357727
verticle: -13.0339, -3.86855, 0 angle : 0.421973
verticle: -13.067, -3.98313, 0 angle : 0.454565
verticle: -13.0678, -4.09688, 0 angle : 0.452407
verticle: -13.0687, -4.21063, 0 angle : 0.482545
verticle: -13.0675, -4.3319, 0 angle : 0.487788
verticle: -13.0361, -4.44482, 0 angle : 0.463094
verticle: -12.9768, -4.54186, 0 angle : 0.421973
verticle: -12.9496, -4.63972, 0 angle : 0.44279
verticle: -12.8622, -4.72087, 0 angle : 0.402026
verticle: -12.8071, -4.80285, 0 angle : 0.383084
verticle: -12.7239, -4.86895, 0 angle : 0.399585
verticle: -12.6105, -4.92668, 0 angle : 0.29074
verticle: -12.5336, -4.97019, 0 angle : 0.30901
verticle: -12.4266, -5.00535, 0 angle : 0.245493
verticle: -12.3237, -5.02544, 0 angle : 0.214891
verticle: -12.2229, -5.03801, 0 angle : 0.132704
verticle: -12.0983, -5.01964, 0 angle : 11.875
verticle: -12.0995, -8.28741, 0 angle : 0.300014
verticle: -12.2304, -8.28319, 0 angle : 0.199792
verticle: -12.327, -8.28568, 0 angle : 0.179137
verticle: -12.4495, -8.31158, 0 angle : 0.121947
verticle: -12.5679, -8.35253, 0 angle : 0.0395647
verticle: -12.6799, -8.41607, 0 angle : 0.0279765
verticle: -12.7598, -8.47878, 0 angle : 0.0442347
verticle: -12.8657, -8.56491, 0 angle : 0.138476
verticle: -12.9372, -8.65773, 0 angle : 0.199792
verticle: -12.9765, -8.74972, 0 angle : 0.214891
verticle: -13.0418, -8.86513, 0 angle : 0.275536
verticle: -13.0749, -8.9797, 0 angle : 0.335718
verticle: -13.0757, -9.09345, 0 angle : 0.359365
verticle: -13.0745, -9.21473, 0 angle : 0.356083
verticle: -13.0733, -9.33601, 0 angle : 0.39217
verticle: -13.0419, -9.44893, 0 angle : 0.428872
verticle: -12.9805, -9.55349, 0 angle : 0.402512
verticle: -12.9211, -9.65052, 0 angle : 0.401538
verticle: -12.8618, -9.74756, 0 angle : 0.417778
verticle: -12.7744, -9.82871, 0 angle : 0.436559
verticle: -12.659, -9.89397, 0 angle : 0.370094
verticle: -12.5758, -9.96007, 0 angle : 0.338041
verticle: -12.4687, -9.99522, 0 angle : 0.384613
verticle: -12.3316, -10.022, 0 angle : 0.265408
verticle: -12.2308, -10.0346, 0 angle : 0.261696
verticle: -12.1041, -10.0237, 0 angle : 7.8231
verticle: -12.1023, -13.1853, 0 angle : 42.4836
Единственный способ решить эту проблему — вычисление расстояния в сочетании с углами, которые превышают определенное значение. Я знаю, что это плохое решение. Но я не могу придумать какой-либо другой способ рассчитать это.
Вот как происходит вычисление угла:
inline float ofVec3f::angle( const ofVec3f& vec ) const {
ofVec3f n1 = this->normalized();
ofVec3f n2 = vec.normalized();
return (float)(acos( n1.dot(n2) )*RAD_TO_DEG);
}
Расстояние между двумя точками:
inline float ofVec3f::distance( const ofVec3f& pnt) const {
float vx = x-pnt.x;
float vy = y-pnt.y;
float vz = z-pnt.z;
return (float)sqrt(vx*vx + vy*vy + vz*vz);
}
Я использовал библиотеку OpenFrameworks, чтобы понять это:
float dist = buildings[x].polygon[z].distance(buildings[x].polygon[z+1]);
float angle ;
if ( z < buildings[x].polygon.size()-1){
angle = buildings[x].polygon[z].angle(buildings[x].polygon[z+1]);
}
if ( ( dist > 0.100)&& ( dist < 0.150)) {
//Is part of ellipse
}
Вот GitHub из библиотеки
https://github.com/openframeworks/openFrameworks/blob/master/libs/openFrameworks/math/ofVec3f.h
Вот два скриншота точек и линии
Вот один векторный массив вершин x, y x, y
-0.11878395,-106.14753 -0.13964462,-38.761494 0.0,0.0 -7.6293945E-6,113.11968 -96.88052,112.56717 -96.79668,85.153725 -97.843834,85.18742 -98.599945,85.107315 -99.58024,84.900116 -100.51039,84.51225 -101.42383,84.06417 -102.06295,83.562485 -102.65193,82.88013 -103.240906,82.197784 -103.77975,81.33476 -104.30187,80.41151 -104.325485,79.56175 -104.59001,78.64513 -104.5802,77.67491 -104.32949,76.77156 -104.07879,75.868195 -103.82809,74.96484 -103.35321,74.18856 -102.63742,73.47914 -102.17926,72.763084 -101.25601,72.24097 -100.59037,71.71221 -99.73398,71.43098 -98.63669,71.2166 -97.83043,71.11605 -96.8,71.14256 -96.859665,45.18112 -97.6492,45.22146 -98.66293,45.134716 -99.64322,44.92752 -100.57338,44.539658 -101.245926,44.158424 -102.12593,43.58989 -102.73163,42.96776 -103.303894,42.22518 -103.84273,41.36216 -104.14067,40.56599 -104.40518,39.649376 -104.412094,38.739384 -104.41901,37.8294 -104.409195,36.859184 -104.15849,35.955826 -103.90778,35.052475 -103.43291,34.27619 -102.71712,33.566765 -102.01806,32.917564 -101.33571,32.328587 -100.445885,31.92691 -99.57278,31.585457 -98.73309,31.364452 -97.68595,31.330748 -96.89641,31.290417 -96.790054,0.056350708 -96.71601,-26.386883 -97.76316,-26.353178 -98.77688,-26.439924 -99.51628,-26.580261 -100.46315,-26.907902 -101.35987,-27.416212 -101.99899,-27.917892 -102.84558,-28.606876 -103.434555,-29.289228 -103.732506,-30.0854 -104.27134,-30.948421 -104.53585,-31.86504 -104.542755,-32.77503 -104.54967,-33.685017 -104.53986,-34.655228 -104.28916,-35.558586 -103.81427,-36.33486 -103.59699,-37.117775 -102.897934,-37.766975 -102.456474,-38.422806 -101.79083,-38.95156 -100.8843,-39.41346 -100.2688,-39.761543 -99.41241,-40.04277 -98.58944,-40.203552 -97.78319,-40.30411 -96.78618,-40.157143 -96.79571,-66.299255 -97.84286,-66.26555 -98.615685,-66.285446 -99.59598,-66.49263 -100.54285,-66.820274 -101.439575,-67.32858 -102.07869,-67.83027 -102.92528,-68.51925 -103.497536,-69.261826 -103.8122,-69.99777 -104.33433,-70.92102 -104.59884,-71.83764 -104.60574,-72.74762 -104.59593,-73.717834 -104.58613,-74.68805 -104.33543,-75.5914 -103.84383,-76.42791 -103.36895,-77.204185 -102.89406,-77.98047 -102.195,-78.62967 -101.27175,-79.151794 -100.6061,-79.68055 -99.74972,-79.96178 -98.65242,-80.17615 -97.84617,-80.27671 -96.83245,-80.189964 -96.81836,-105.482315 -0.11878395,-106.14753
Другой векторный массив
0.0,46.766045 -5.8214893,46.69686 -5.820862,47.05351 -5.8475914,47.425262 -5.918213,47.749863 -6.0161915,48.08957 -6.1278477,48.43683 -6.283396,48.73693 -6.4526215,49.04459 -6.6794205,49.312645 -6.89254,49.573143 -7.1330166,49.848755 -7.4037094,50.069653 -7.6744003,50.290554 -7.988985,50.4643 -8.32011,50.57577 -8.621017,50.74196 -8.982357,50.79873 -9.330019,50.847942 -9.677681,50.897156 -10.011665,50.938812 -35.375645,50.81018 -64.38959,50.69822 -64.377785,49.620728 -64.35231,48.535683 -64.299484,47.435524 -64.20275,46.382523 -64.064995,45.30686 -63.91356,44.223648 -63.748447,43.132874 -63.525764,42.081707 -63.2894,41.022987 -63.025684,39.949158 -62.71807,38.922485 -62.38311,37.880703 -62.004246,36.886078 -61.611713,35.883904 -61.191822,34.86661 -60.758247,33.841774 -60.280785,32.86409 -59.759426,31.933561 -59.224392,30.995481 -58.67568,30.049845 -58.08307,29.151367 -57.476788,28.245333 -56.856827,27.331745 -56.162758,26.520025 -55.48522,25.646042 -54.777473,24.826767 -54.02583,24.05465 -53.304405,23.227821 -52.508865,22.502861 -51.69965,21.770344 -50.890438,21.037828 -50.051006,20.360025 -49.1979,19.674667 -48.314575,19.044018 -47.401035,18.468079 -46.504032,17.829878 -45.560276,17.30865 -44.602844,16.77987 -43.65909,16.258642 -42.671436,15.784572 -41.697464,15.318055 -40.693275,14.906249 -39.689087,14.494442 -38.654682,14.137346 -37.633957,13.787806 -36.58301,13.492973 -35.545746,13.205697 -34.478268,12.973131 -33.42446,12.748117 -32.340443,12.577815 -31.270102,12.415068 -30.18322,12.314583 -29.09634,12.2141 -28.006598,12.183435 -26.916859,12.152769 -25.840796,12.129659 -25.80352,9.967116 -25.811121,8.75754 -25.813,7.687599 -25.713875,0.20740414 -25.278425,0.25250435 -12.768033,0.054601192 -0.25477973,-0.073483296 0.0,0.0 0.0,46.766045
Решение
Подгонка по кругу Hough или RANSAC, вероятно, подойдет вам; При обработке изображений мы используем эти алгоритмы для поиска окружностей, дуг, эллипсов и других фигур.
http://en.wikipedia.org/wiki/Hough_transform
http://en.wikipedia.org/wiki/RANSAC
Эти алгоритмы хорошо работают с зашумленными данными.
В книге Гэри Брэдски «Изучение OpenCV» есть раздел, озаглавленный «Преобразование Hough Circle», который занимает несколько страниц. Хотя вы можете взглянуть на саму библиотеку OpenCV, вы, вероятно, найдете более простые описания преобразования Хафа и RANSAC в других местах.
[РЕДАКТИРОВАТЬ]
Я написал быстрый алгоритм Хафа на C #, и он хорошо работал с вашими данными. Вы можете добавить случайный шум, и он все равно будет работать. Основной алгоритм содержит около 100 строк кода с комментариями и пробелами, и это неаккуратный алгоритм.
Часть выходного изображения из этого алгоритма показана ниже с точками данных в белом и кружками Hough fit в красном.
Один стандартный алгоритмический шаг, который я не реализовал, — это фильтрация данных, чтобы исключить все, кроме наилучшего совпадения окружности, когда есть несколько разумных совпадений окружности с примерно одинаковым центром и примерно одинаковым радиусом. Вот почему вы видите двойной круг, проходящий через точки.
Хотя алгоритм Hough может показаться излишним, приятно то, что он будет работать снова и снова, его можно многократно использовать, его легко параметризировать, и он даст хорошие результаты независимо от того, чистые данные или шумные.
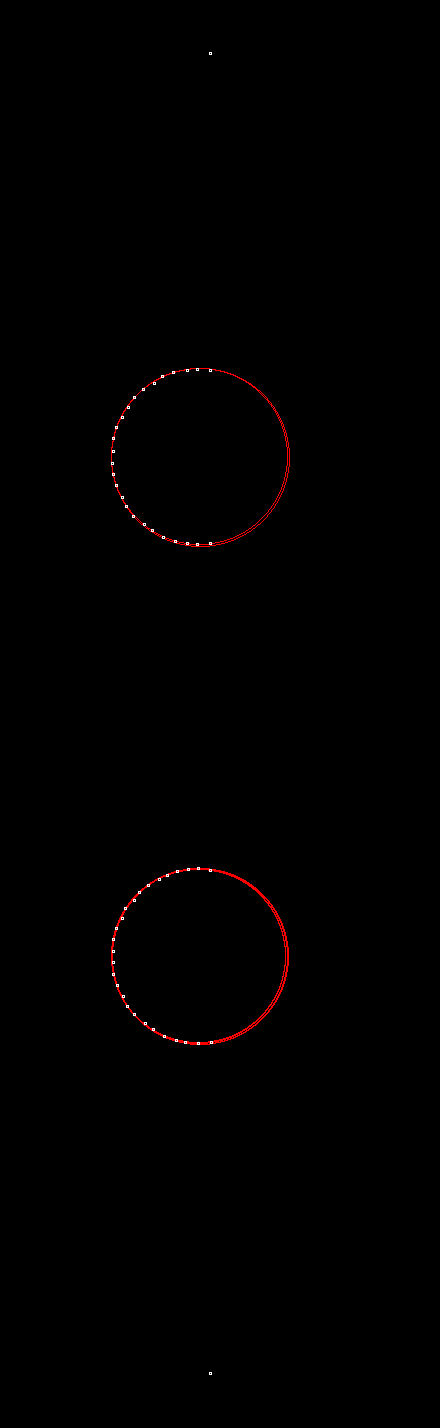
ПРИМЕЧАНИЕ: чтобы упростить реализацию, я преобразовал значения с плавающей точкой для (x, y) в целые числа и нормализовал значения так, чтобы все (x, y) были положительными. Что-то вроде этого:
int x = (int)(100 * floatX + 1600); //floatX = original X value in data
int y = (int)(100 * floatY + 3200); //floatY = original Y value in data
Другие решения
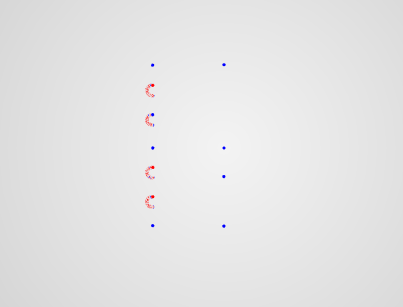
это не полный ответ, а иллюстрация моего комментария, в котором я нахожу центры дуг успешных точек … методом проб и ошибок лучше всего работать, если вы посмотрите на более широкие точки разброса (1,5,9), (2,6,10 ) и т. д. (данные представляют собой список ваших пар х, у)
arccenter[p_] := {xc, yc} /.
Solve[ { (p[[1]] - p[[2]] ).({xc, yc} - (p[[1]] + p[[2]])/2) ==
0, (p[[2]] - p[[3]] ).({xc, yc} - (p[[2]] + p[[3]])/2) ==
0 } , {xc, yc}][[1]]
pdata = Partition[data, 9, 1];
centers = arccenter[#[[{1, 5, 9}]]] & /@ pdata;
cc = Select[centers, Abs[#[[1]]] < 30 && Abs[#[[2]]] < 30 &];
Show[
{Graphics[Point[#] & /@ data],
Graphics[{Red, Point[#]} & /@ cc]},
PlotRange -> {{-20, 0}, {-15, 15}}]

нужно просто немного больше усилий отфильтровать, какие центры находятся рядом друг с другом.
(напомним, что они тоже заказаны ..)
