Обеспечение ICP, внутренние метрики
Итак, у меня есть итерационная ближайшая точка (ICP) алгоритм, который был написан и подгонит модель к облаку точек. В качестве краткого руководства для тех, кто не в курсе, ICP представляет собой простой алгоритм, который подбирает точки к модели, в конечном итоге предоставляя однородную матрицу преобразования между моделью и точками.
Вот краткий учебник по картинкам.
Шаг 1. Найдите ближайшую точку в наборе модели для вашего набора данных:
Шаг 2: Используя несколько забавных математических упражнений (иногда основанных на градиентном спуске или SVD), притяните облака ближе друг к другу и повторяйте, пока не будет сформирована поза:
![Рисунок 2] [2]
Теперь это немного просто и работает, что я хотел бы помочь с:
Как мне узнать, хорошая ли у меня поза?
Так что в настоящее время у меня есть две идеи, но они вроде хакерские:
-
Сколько точек в алгоритме ICP. Т.е., если я подхожу почти без очков, я предполагаю, что поза будет плохой:
Но что, если поза действительно хороша? Это может быть даже с несколькими очками. Я не хочу отказываться от хороших поз:
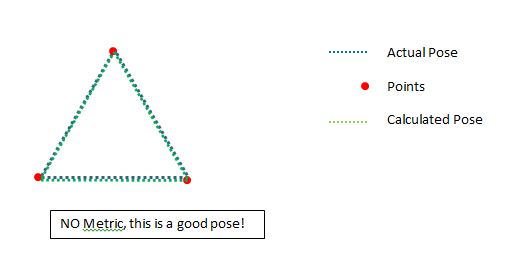
Итак, что мы видим здесь, так это то, что низкие точки могут действительно занять очень хорошую позицию, если они находятся в нужном месте.
Таким образом, другой исследуемой метрикой было отношение предоставленных точек к используемым точкам. Вот пример
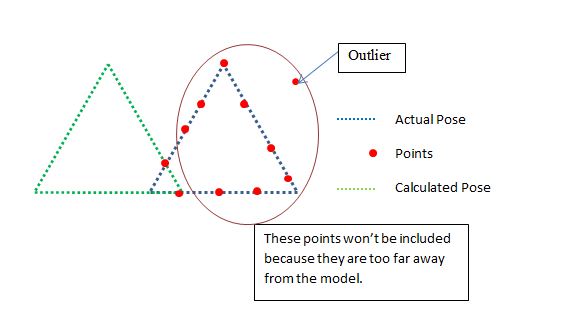
Теперь мы исключаем пункты, которые находятся слишком далеко, потому что они будут отклоняться, теперь это означает, что нам нужна хорошая стартовая позиция для работы ПМС, но я в порядке с этим. Теперь в приведенном выше примере уверенность скажет «НЕТ», это плохая поза, и это было бы правильно, потому что соотношение очков к включенным точкам:
2/11 < SOME_THRESHOLD
Так что это хорошо, но это не удастся в случае, показанном выше, где треугольник перевернут. Это скажет, что треугольник с ног на голову хорош, потому что все точки используются ICP.
Вы не Нужно быть экспертом по ICP, чтобы ответить на этот вопрос, я ищу хорошие идеи. Используя знание пунктов, как мы можем классифицировать, является ли это хорошим решением для позы или нет?
Совместное использование обоих этих решений в тандеме является хорошим предложением, но, если вы спросите меня, это довольно слабое решение, очень глупое, чтобы просто ограничить его.
Какие есть хорошие идеи, как это сделать?
PS. Если вы хотите добавить код, пожалуйста, сделайте это. Я работаю в C ++.
PPS. Кто-то помог мне пометить этот вопрос, я не уверен, где он должен упасть.
Решение
Одним из возможных подходов может быть сравнение поз по их формам и ориентации.
Сравнение форм может быть сделано с Хаусдорфово расстояние до изометрии, то есть позы имеют одинаковую форму, если
d(I(actual_pose), calculated_pose) < d_threshold
где d_threshold должно быть найдено из экспериментов. В качестве изометрических модификаций X я бы рассматривал повороты на разные углы — в данном случае кажется достаточным.
Если позы имеют одинаковую форму, мы должны сравнить их ориентацию. Для сравнения ориентации мы могли бы использовать несколько упрощенный Модель Фрекса. Для каждой позы мы должны рассчитать значения
{x_y min, x_y max, x_z min, x_z max, y_z min, y_z max}
а затем убедитесь, что каждое различие между соответствующими значениями для поз не нарушается another_thresholdтакже получено из экспериментов.
Надеюсь, это имеет какой-то смысл, или, по крайней мере, вы можете извлечь из этого что-то полезное для ваших целей.
Другие решения
ICP пытается минимизировать расстояние между вашим облаком точек и моделью, да? Разве не имеет смысла оценивать его на основе того, что это расстояние на самом деле после выполнения?
Я предполагаю, что он пытается минимизировать сумму квадратов расстояний между каждой точкой, которую вы пытаетесь подогнать, и ближайшей модельной точкой. Поэтому, если вы хотите получить показатель качества, почему бы просто не нормализовать эту сумму, разделив ее на количество подходящих точек. Да, выбросы будут несколько нарушать его, но они также могут несколько нарушить ваше состояние.
Кажется, что любой расчет, который вы можете придумать, который дает больше понимания, чем тот, который сводит к минимуму ICP, был бы более полезным, встроен в сам алгоритм, поэтому он также может минимизировать это. знак равно
Обновить
Я думаю, что я не совсем понял алгоритм. Кажется, что он итеративно выбирает подмножество точек, преобразует их, чтобы минимизировать ошибку, а затем повторяет эти два шага? В этом случае ваше идеальное решение выбирает как можно больше точек, сохраняя при этом как можно меньшую ошибку.
Вы сказали, что объединение двух терминов кажется слабым решением, но для меня это звучит как точное описание того, что вы хотите, и оно отражает две основные особенности алгоритма (да?). Оценка с использованием чего-то вроде error + B * (selected / total) Духовно похоже на то, как регуляризация используется для решения проблемы переоснащения с помощью алгоритмов ML с градиентным спуском (и подобных). Выбор хорошего значения для B потребует некоторых экспериментов.
Глядя на ваши примеры, кажется, что одним из факторов, определяющих, является ли совпадение хорошим или нет, является качество очков. Не могли бы вы использовать / рассчитать весовой коэффициент при расчете вашей метрики?
Например, вы могли бы придавить точкам вниз коллинеарные / копланарные или пространственно близкие, поскольку они, вероятно, определяют одну и ту же особенность. Это, возможно, позволит отклонить ваш перевернутый треугольник (так как точки находятся на одной линии, и это не является хорошим показателем общей позы), но угловой случай будет в порядке, поскольку они приблизительно определяют корпус.
В качестве альтернативы, возможно, вес должен быть на том, как распределены точки вокруг позы, снова пытаясь гарантировать, что у вас есть хороший охват, вместо того, чтобы соответствовать маленьким нечетким признакам.
