Ньютон Рафсон с SSE2 — может кто-нибудь объяснить мне эти 3 строки
Я читаю этот документ: http://software.intel.com/en-us/articles/interactive-ray-tracing
и я наткнулся на эти три строки кода:
SIMD-версия уже немного быстрее, но мы можем добиться большего.
Intel добавила быструю функцию 1 / sqrt (x) в набор инструкций SSE2.
Единственным недостатком является то, что его точность ограничена. Нам нужно
точность, поэтому мы уточняем это с помощью Newton-Rhapson:
__m128 nr = _mm_rsqrt_ps( x );
__m128 muls = _mm_mul_ps( _mm_mul_ps( x, nr ), nr );
result = _mm_mul_ps( _mm_mul_ps( half, nr ), _mm_sub_ps( three, muls ) );
Этот код предполагает существование переменной __m128 с именем ‘half’
(четыре раза по 0,5f) и переменная «три» (четыре раза по 3,0f).
Я знаю, как использовать Ньютона Рафсона для вычисления нуля функции, и я знаю, как использовать его для вычисления квадратного корня числа, но я просто не вижу, как этот код выполняет его.
Может кто-нибудь объяснить мне, пожалуйста?
Решение
Учитывая итерацию Ньютона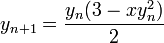 
,должно быть довольно просто увидеть это в исходном коде.
__m128 nr = _mm_rsqrt_ps( x ); // The initial approximation y_0
__m128 muls = _mm_mul_ps( _mm_mul_ps( x, nr ), nr ); // muls = x*nr*nr == x(y_n)^2
result = _mm_mul_ps(
_mm_sub_ps( three, muls ) // this is 3.0 - mul;
/*multiplied by */ __mm_mul_ps(half,nr) // y_0 / 2 or y_0 * 0.5
);
А если быть точным, этот алгоритм для обратный квадратный корень.
Обратите внимание, что это до сих пор не дает полностью точный результат. rsqrtps с итерацией NR дает почти 23 бита точности, по сравнению с sqrtps24 бита с правильным округлением для последнего бита.
Ограниченная точность является проблемой, если вы хотите усечь результат до целого числа. (int)4.99999 является 4, Кроме того, следите за x == 0.0 случай, если с помощью sqrt(x) ~= x * sqrt(x), так как 0 * +Inf = NaN,
Другие решения
Чтобы вычислить обратный квадратный корень из a, Метод Ньютона применяется к уравнению 0=f(x)=a-x^(-2) с производной f'(x)=2*x^(-3) и, таким образом, шаг итерации
N(x) = x - f(x)/f'(x) = x - (a*x^3-x)/2
= x/2 * (3 - a*x^2)
Этот метод без деления имеет — в отличие от глобально сходящихся Метод Герона — ограниченная область сходимости, поэтому вам нужно уже хорошее приближение обратного квадратного корня, чтобы получить лучшее приближение.