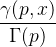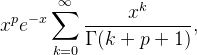Неполный алгоритм гамма-функции

Question

Неполный алгоритм гамма-функции

Существует очень краткий алгоритм для вычисления нижней неполной гамма-функции:

https://people.sc.fsu.edu/~jburkardt/f_src/asa147/asa147.html

Мы закодировали это в C ++. В этом алгоритме есть одна вещь, которую я не понимаю. В одном месте вычислить следующее выражение:

$\ Гидроразрыва {\ гамма (р, х)} {\ Gamma (р)}$

он заменяется на:

$x ^ pe ^ {- x} \ sum ^ \ infty_ {k = 0} \ гидроразрыва {х ^ к} {\ Gamma (к + р + 1)},$

Очевидно, это то же самое, но почему это делается так? Вычисление exp из lgamma более эффективно, чем вычисление функции tgamma (оба lgamma а также tgamma доступны в C ++)?

0

c++gamma-function

Решение

Другие решения

Является ли вычисление exp из lgamma более эффективным, чем вычисление функции tgamma (в C ++ доступны и lgamma, и tgamma)?

вычисление lgamma более эффективно, потому что это в основном поведение n * log (n).
Поэтому, как правило, у вас есть хороший идентификатор приближения, который вы пытаетесь вычислить
функция lgamma (x) / x.

также имейте в виду, что lgamma часто используется, потому что это часть выражения, которое может быть вычислено в то время как tgamma, который растет так же быстро, как факториал, нет. Так что вычислить целое выражение безопасно f(x) как exp (log (f (x))), и если f (x) имеет произведение tgammaтогда log (f (x)) придется суммировать / вычитать lgamma,

Хороший способ избежать переполнения, в основном

1

Источник

Accepted Answer

Вы найдете правильные реализации Gamma для C ++ здесь:
http://www.boost.org/doc/libs/1_64_0/libs/math/doc/html/math_toolkit/sf_gamma

1