Не могу понять эту строку в треугольнике Паскаля для переполнения стека
Я должен написать код, который генерирует треугольник Паскаля с 12 строками.
Я написал все сам, кроме одной части. Это формула, которую мы используем для генерации чисел. И проблема в том, что я не понимаю, какова связь между нашими счетчиками и сгенерированными числами (так как мы используем наши счетчики.).
#include <iostream>
#include <string>
using namespace std;
int main() {
const int rows=12;
int padding, value, fxValue;
for(int rowCounter=0; rowCounter<rows; rowCounter++)
{
fxValue=1;
cout << string((rows-rowCounter)*6, ' ');
for(int fxCounter=0; fxCounter<=rowCounter; fxCounter++)
{
value=fxValue;
fxValue = fxValue*(rowCounter-fxCounter)/(fxCounter+1);
// cout << "fxCounter: "<< fxCounter << endl
// << "rowCounter: " << rowCounter << endl
// << "fxCounter: " << fxCounter << endl
// << "fxValue: " << fxValue << endl;
padding=fxValue/10;
if(padding==0) cout << value << string(11, ' ');
else if(10>padding) cout << value << string(10, ' ');
else if(padding>10) cout << value << string(9, ' ');
}
cout << endl;
}
return 0;
}
Вот проблема:
fxValue = fxValue*(rowCounter-fxCounter)/(fxCounter+1);
Может кто-нибудь объяснить, как автор пришел к мысли об использовании этих переменных и как он работает нормально?
Решение
Это работает, потому что треугольник Паскаля может быть представлен с биномиальными коэффициентами:
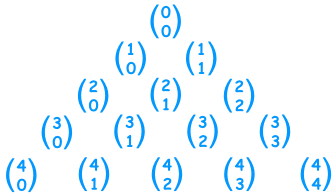
Эта формула в вашем коде основана на том факте, что для того же n-индекса (в случае треугольника Паскаля та же строка), чтобы получить следующий элемент (k -> k + 1), нам нужно умножить текущее значение (nk) / (k + 1):
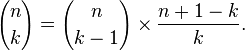
Это довольно легко доказать, если вы хотите убедить себя в этом.
Таким образом, вы можете получить следующее значение из предыдущего с помощью этой операции.
Другие решения
