Не могу понять этот алгоритм простого генератора в моем учебнике
Я изучаю элементы программирования интервью, и я застрял на проблеме.
Речь идет о написании функции c ++ для нахождения всех простых чисел от 1 до n для данного n.
vector<int> generate_primes_from_1_to_n(const int &n) {
int size = floor(0.5 * (n - 3)) + 1;
// is_prime[i] represents (2i+3) is prime or not
vector<int> primes; // stores the primes from 1 to n
primes.push_back(2);
vector<bool> is_prime(size, true);
for(long i = 0; i < size; ++i) {
if(is_prime[i]) {
int p = (i << 1) + 3;
primes.push_back(p);
// sieving from p^2, whose index is 2i^2 + 6i + 3
for (long j = ((i * i) << 1) + 6 * i + 3; j < size; j += p) {
is_prime[j] = false;
}
}
}
}
В частности, я не могу понять прокомментированное «просеивание из p ^ 2, чей индекс равен 2i ^ 2 + 6i + 3». Что касается других частей, я могу понять примерное представление о том, как они работают, но я не знаю, откуда взялся этот «2i ^ 2 + 6i + 3», что он делает, и как это и связанные с ним части коды работают.
Кто-нибудь может объяснить этот код лучше?
Спасибо.
+
Я получаю этот вывод (+ ‘Cout’s, чтобы понять это лучше)
./a.out 100
size is: 49
for i = 0 is_prime[i] is 1
pushing back p of size 3
((i * i) << 1) + 6 * i + 3 for i of 0 is 3
((i * i) << 1) + 6 * i + 3 for i of 0 is 6
((i * i) << 1) + 6 * i + 3 for i of 0 is 9
((i * i) << 1) + 6 * i + 3 for i of 0 is 12
((i * i) << 1) + 6 * i + 3 for i of 0 is 15
((i * i) << 1) + 6 * i + 3 for i of 0 is 18
((i * i) << 1) + 6 * i + 3 for i of 0 is 21
((i * i) << 1) + 6 * i + 3 for i of 0 is 24
((i * i) << 1) + 6 * i + 3 for i of 0 is 27
((i * i) << 1) + 6 * i + 3 for i of 0 is 30
((i * i) << 1) + 6 * i + 3 for i of 0 is 33
((i * i) << 1) + 6 * i + 3 for i of 0 is 36
((i * i) << 1) + 6 * i + 3 for i of 0 is 39
((i * i) << 1) + 6 * i + 3 for i of 0 is 42
((i * i) << 1) + 6 * i + 3 for i of 0 is 45
((i * i) << 1) + 6 * i + 3 for i of 0 is 48
for i = 1 is_prime[i] is 1
pushing back p of size 5
((i * i) << 1) + 6 * i + 3 for i of 1 is 11
((i * i) << 1) + 6 * i + 3 for i of 1 is 16
((i * i) << 1) + 6 * i + 3 for i of 1 is 21
((i * i) << 1) + 6 * i + 3 for i of 1 is 26
((i * i) << 1) + 6 * i + 3 for i of 1 is 31
((i * i) << 1) + 6 * i + 3 for i of 1 is 36
((i * i) << 1) + 6 * i + 3 for i of 1 is 41
((i * i) << 1) + 6 * i + 3 for i of 1 is 46
for i = 2 is_prime[i] is 1
pushing back p of size 7
((i * i) << 1) + 6 * i + 3 for i of 2 is 23
((i * i) << 1) + 6 * i + 3 for i of 2 is 30
((i * i) << 1) + 6 * i + 3 for i of 2 is 37
((i * i) << 1) + 6 * i + 3 for i of 2 is 44
for i = 3 is_prime[i] is 0
for i = 4 is_prime[i] is 1
pushing back p of size 11
for i = 5 is_prime[i] is 1
pushing back p of size 13
for i = 6 is_prime[i] is 0
for i = 7 is_prime[i] is 1
pushing back p of size 17
for i = 8 is_prime[i] is 1
pushing back p of size 19
for i = 9 is_prime[i] is 0
for i = 10 is_prime[i] is 1
pushing back p of size 23
for i = 11 is_prime[i] is 0
for i = 12 is_prime[i] is 0
for i = 13 is_prime[i] is 1
pushing back p of size 29
for i = 14 is_prime[i] is 1
pushing back p of size 31
for i = 15 is_prime[i] is 0
for i = 16 is_prime[i] is 0
for i = 17 is_prime[i] is 1
pushing back p of size 37
for i = 18 is_prime[i] is 0
for i = 19 is_prime[i] is 1
pushing back p of size 41
for i = 20 is_prime[i] is 1
pushing back p of size 43
for i = 21 is_prime[i] is 0
for i = 22 is_prime[i] is 1
pushing back p of size 47
for i = 23 is_prime[i] is 0
for i = 24 is_prime[i] is 0
for i = 25 is_prime[i] is 1
pushing back p of size 53
for i = 26 is_prime[i] is 0
for i = 27 is_prime[i] is 0
for i = 28 is_prime[i] is 1
pushing back p of size 59
for i = 29 is_prime[i] is 1
pushing back p of size 61
for i = 30 is_prime[i] is 0
for i = 31 is_prime[i] is 0
for i = 32 is_prime[i] is 1
pushing back p of size 67
for i = 33 is_prime[i] is 0
for i = 34 is_prime[i] is 1
pushing back p of size 71
for i = 35 is_prime[i] is 1
pushing back p of size 73
for i = 36 is_prime[i] is 0
for i = 37 is_prime[i] is 0
for i = 38 is_prime[i] is 1
pushing back p of size 79
for i = 39 is_prime[i] is 0
for i = 40 is_prime[i] is 1
pushing back p of size 83
for i = 41 is_prime[i] is 0
for i = 42 is_prime[i] is 0
for i = 43 is_prime[i] is 1
pushing back p of size 89
for i = 44 is_prime[i] is 0
for i = 45 is_prime[i] is 0
for i = 46 is_prime[i] is 0
for i = 47 is_prime[i] is 1
pushing back p of size 97
for i = 48 is_prime[i] is 0
Это также не имеет смысла для меня.
Например, почему при p = 5 он начинает удалять его с 11, а не 5 ^ 2 = 25, в строках ниже?
отталкивая р размера 5
((я * я) << 1) + 6 * i + 3 для i из 1 — 11
Кроме того, разве 11 не простое число?
Это действительно сбивает с толку.
Пожалуйста, помогите мне.
Спасибо.
Решение
Алгоритм
Алгоритм, используемый вашим основным генератором кода, называется «Сито Эратосфена». Как правило, он создает список чисел и выполняет итерации по списку. Все умножения текущего числа удаляются из списка, а остальные числа простые.
Например, давайте рассмотрим [2,3,4,5,6,7,8,9,10,11,12,13,14,15], Мы сталкиваемся с 2, поэтому мы удаляем все четные числа из списка:
[2,3,5,7,9,11,13,15]
То же самое для 3:
[2,3,5,7,11,13]
5, 7, 11 а также 13 в списке нет умножений, поэтому мы ничего не удаляем и остаемся со списком простых чисел.
Визуальный пример
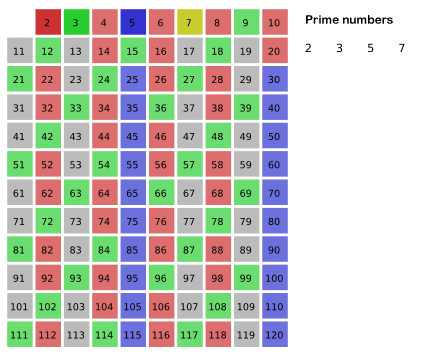
В этом примере (любезно предоставлено Википедией) все умножения 2, 3 и 5 были удалены из списка — умножения 2 были окрашены в розовый цвет, умножения 3 были окрашены в зеленый, а умножения 5 в темно-синий. 7 будет повторен следующим, поэтому он выделен. Числа темного цвета просты, числа светлого цвета не просты, а серые числа еще не достигнуты.
Оптимизации в вашем коде
Как уже упоминалось @BenJackson, ваш код оптимизирован дважды:
- Во-первых, он хранит только нечетные числа, начиная только с 3, потому что мы знаем, что четные числа не являются простыми (кроме 2).
- Во-вторых, для числа p он только начинает просеивать от p². Это правильно, потому что если
n<pзатемn*pбыл уже просеян, когда умноженияnбыли просеяны.
Это причина, почему загадочный комментарий:
// sieving from p^2, whose index is 2i^2 + 6i + 3
Предположим, что наш алгоритм достиг второго элемента в векторе, поэтому i=2, Количество в вопросе 5, потому что индекс i обозначает число 2i+3 (первая оптимизация).
Мы должны просеять все умножения 5 от 25 и далее. Индекс, который представляет 25 является 11, так как 25=2*11+3, После ваших распечаток он удаляет индексы 11, 16, 21, 26, ..., которые соответствуют номерам 25, 35, 45, 55, .. — все нечетные умножения 5 мы хотели бы удалить.
Вы можете прочитать больше об этом на Википедия или же Wolfram MathWorld, и есть хороший javascript он-лайн демонстрация здесь.
Другие решения
В таблице простых чисел хранятся только нечетные значения, начиная с 3 (очевидно, четные значения не могут быть простыми). Отношение дается в строке int p = (i << 1) + 3, или же p = 2i + 3, Теперь решите это для i, получая i = (p - 3)/2, Что теперь i соответствует p^2? Подключите (2i+3)^2 к этой второй формуле и упростить. Теперь у вас есть i за p^2 с точки зрения i за p,
Пример: допустим i=1, таким образом, запись is_prime[i] это тест прайма p=2i+3, или же p=5, Так что да, это просто. Теперь сейв (объясненный в другом месте) хочет начать отмечать не простые числа в 25. Он должен знать, что i соответствует 25. Теперь вы можете просто вычислить p*p а затем вставить это в i=(p-3)/2 и получить j=11, Код пропустил эти промежуточные шаги (как я показал выше) для вычисления j=2i^2+6i+3 и получил j=11 непосредственно.
Линии, подобные этим:
vector<int> generate_primes_from_1_to_n(const int &n) {
int size = floor(0.5 * (n - 3)) + 1;
…
for(long i = 0; i < size; ++i) {
if(is_prime[i]) {
int p = (i << 1) + 3;
являются «взломом», так что потенциальные простые числа 3, 5, 7 и т. д. могут быть перебраны, повторяя 0, 1, 2, 3 в i и используя p для соответствующих возможных простых чисел 3, 5, 7, 9 и т. д.
Это основное простое сито, кроме этого.
Как отметили другие, я карты массив мест и п сопоставляет числа, которые представляют эти местоположения массива, согласно формуле п = 2 я + 1. Может быть легче подумать, если вы продолжите я а также п явно в программе:
function primes(n)
m := floor((n-1)/2)
sieve := makeArray(0..m-1, True)
i := 0; p := 3; ps := [2]
while p * p <= n
if sieve[i]
append p to ps
j := (p*p - 3) / 2
while j < m
sieve[j] := False
j := j + p
i := i + 1; p := p + 2
while i < m
if sieve[i]
append p to ps
i := i + 1; p := p + 2
return ps
Странная формула для J в исходном коде формируется по формуле J показано выше и переписать с точки зрения я вместо п.
Если вы заинтересованы в программировании с простыми числами, у меня есть сочинение в моем блоге, который, среди прочего, обсуждает эту точную формулу в некоторой глубине.
