Найти 2 подмножества в массиве с минимальной разностью и последовательными элементами

Question

Найти 2 подмножества в массиве с минимальной разностью и последовательными элементами

Я столкнулся с вариацией проблемы подмножества сумм, которая мне кажется довольно интересной. Таким образом, учитывая массив (положительных) элементов, вы должны разбить его на 2 набора, чтобы их разница была минимальной. Но здесь есть подвох. Элементы должны быть последовательными, и они также работают в круговом порядке. Вот 2 примера, чтобы вы могли понять, что я имею в виду:

ПРИМЕР 1:

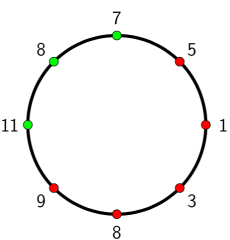
ВХОД: 7 5 1 3 8 9 11 8

ВЫХОД: 0 (набор 1: {11,8,7}, набор 2: {5,1,3,8,9}

результирующая картинка .

ПРИМЕР 2:

ВХОД: 10 14 75 90 3 5 40 4 8

ВЫХОД: 27 (набор 1: {4,8,10,14,75}, набор 2: {90,3,5,40})

Что такое возможное решение с использованием C ++? Спасибо!

-1

algorithm c++c++11 knapsack-problem subset-sum

Решение

Другие решения

Других решений пока нет …

Источник

Accepted Answer

Есть линейное решение с использованием двух указателей. Целевым параметром является диапазон с суммой, максимально приближенной к сумме остальных.

Установите оба индекса left, right в начало массива. csum текущая сумма диапазона массива left..right-1,

Если добавление еще одного элемента приближает текущее значение к идеальному, переместите правый указатель и обновите параметры.

Когда добавление элемента ухудшает текущую сумму, начинайте удалять левые элементы.

Delphi-код возвращает только лучшую разницу, сам диапазон ((left,right-1) пара) можно найти в собственной реализации Min операция.

  function Nice(A: TArray<Integer>): Integer;
var
left, right, i, sum, csum, diff: Integer;
begin
sum := 0;
for i := 0 to High(A) do
sum := sum + A[i];

left := 0;
right := 1;
csum := A[0]; //sum of current subsequence
diff := Abs(sum - 2 * csum); //dif = Abs((sum - csum) - csum)
result := diff;

repeat

//if adding right element makes difference better
while (right < Length(A)) and (Abs(sum - 2 * (csum + A[right])) < diff) do begin
csum := csum + A[right];
diff := Abs(sum - 2 * csum);
result := Min(result, diff);
right := right + 1;
end;

repeat
csum := csum - A[left];  //we always need at least one step
diff := Abs(sum - 2 * csum);
result := Min(result, diff);
left := left + 1;
until (left = right) or (Abs(sum - 2 * (csum - A[left])) >= diff);

until (left = right);

end;

3