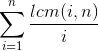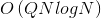Наиболее эффективный алгоритм для нахождения этого суммирования LCM

Проблема: найти

Диапазон N : 1<= n <знак равно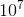

Основная проблема — обработка запросов (Q), которые могут быть большими. 1 <= Q <знак равно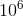

Методы, которые я использовал до сих пор:

Грубая сила

while(Q--)
{
int N;
cin>>N;
for(int i=1;i<=N;i++)
ans += lcm(i,N)/i ;
}

Сложность:

Предварительная обработка и обработка запросов в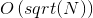

Сначала я строю таблицу, в которой содержится значение функции Эйлера для каждого N.
Это можно сделать за O (N).

void sieve()
{
// phi table holds euler totient function value
// lp holds the lowest prime factor for a number
// pr is a vector which contains prime numbers
phi[1]=1;
for(int i=2;i<=MAX;i++)
{
if(lp[i]==0)
{
lp[i]=i;
phi[i]=i-1;
pr.push_back(i);
}
else
{
if(lp[i]==lp[i/lp[i]])
phi[i] = phi[i/lp[i]]*lp[i];
else phi[i] = phi[i/lp[i]]*(lp[i]-1);
}
for(int j=0;j<(int)pr.size()&&pr[j]<=lp[i]&&i*pr[j]<=MAX;j++)
lp[i*pr[j]] = pr[j];
}

Для каждого запроса разложить N и добавить d*phi[d] к результату.

for(int i=1;i*i<=n;i++)
{
if(n%i==0)
{
// i is a factor
sum += (n/i)*phi[n/i];
if(i*i!=n)
{
// n/i is a factor too
sum += i*phi[i];
}
}
}

Это занимает O (sqrt (N)).

Сложность: O (Q * sqrt (N))

Обработка запросов в O (1)

К описанному выше методу сита я добавляю часть, которая вычисляет нужный нам ответ в O (NLogN)

for(int i=1;i<=MAX;++i)
{
//MAX is 10^7
for(int j=i;j<=MAX;j+=i)
{
ans[j] += i*phi[i];
}
}

Это, к сожалению, истекает для заданных ограничений и ограничения по времени (1 секунда).

Я думаю, что это включает в себя некоторую умную идею относительно факторизации N.
Я могу просторизовать число в O (LogN), используя построенную выше таблицу lp (наименьшее простое число), но я не могу понять, как получить ответ, используя факторизацию.