На гексагональной сетке: выбор плиток в пределах заданного радиуса точки выбора.
Я разрабатываю простую 2D настольную игру с использованием гексагональных карт тайлов, я прочитал несколько статей (в том числе об игре, которые связаны каждый раз, когда возникает вопрос о гексагональных тайлах) о том, как рисовать гексы на экране и как управлять движение (хотя многое из этого я уже сделал раньше). Моя главная проблема — найти соседние плитки на основе заданного радиуса.
Вот как работает моя картографическая система:
(0,0) (0,1) (0,2) (0,3) (0,4)
(1,0) (1,1) (1,2) (1,3) (1,4)
(2,0) (2,1) (2,2) (2,3) (2,4)
(3,0) (3,1) (3,2) (3,3) (3,4) etc...
С чем я борюсь, так это с тем, что я не могу просто «выбрать» соседние плитки, используя for(x-range;x+range;x++); for(y-range;y+range;y++); потому что он выбирает ненужные тайлы (в примере, который я дал, выбор плитки (1,1) и диапазон 1 также дал бы мне плитку (3,0) (те, которые мне действительно нужны, были (0,1) ( 0,2) (1,0) (1,2) (2,1) (2,2)), что вроде как рядом с плиткой (из-за структуры массива), но это не совсем то, что я хочу чтобы выбрать. Я мог бы просто грубо заставить его, но это было бы не красиво и, вероятно, не охватило бы все аспекты «выбора радиуса».
Может ли кто-нибудь указать мне правильное направление здесь?
Решение
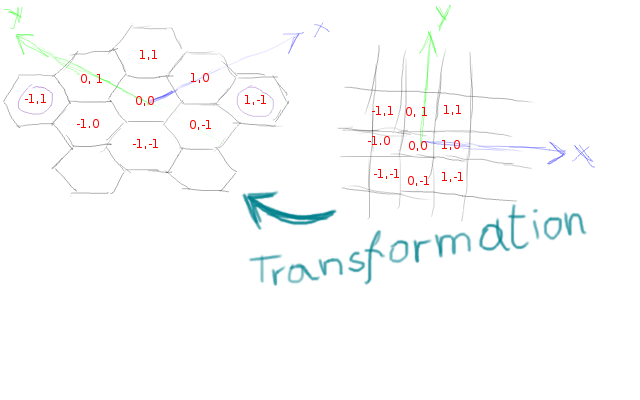
Что такое гексагональная сетка?
То, что вы видите выше, это две сетки. Все дело в том, как вы нумеруете свои плитки и как вы понимаете, что такое шестиугольная сетка. На мой взгляд, шестиугольная сетка — не более чем деформированная ортогональная.
Те две шестигранные плитки, которые я обведу фиолетовым, теоретически все еще примыкают к 0,0, Однако, из-за деформации, которую мы прошли, чтобы получить сетку с шестигранной плиткой из ортогональной, эти два больше не являются визуально смежны.
деформация
Нам нужно понять, что деформация произошла в определенном направлении, вдоль [(-1,1) (1,-1)] мнимая линия в моем примере. Чтобы быть более точным, это как если бы сетка была вытянута вдоль этой линии, и раздавленный вдоль линии, перпендикулярной к этому. Естественно, две плитки на этой линии разложены и больше не являются визуально смежными. И наоборот, плитка (1, 1) а также (-1, -1) которые были по диагонали (0, 0) сейчас необычно близки к (0, 0)так близко, что они сейчас визуально смежный в (0, 0), Однако математически они все еще являются диагоналями, и это помогает обрабатывать их в вашем коде таким образом.
выбор
Изображение, которое я показываю, иллюстрирует радиус 1. Для радиуса два вы заметите (2, -2) а также (-2, 2) являются плитки, которые не должны быть включены в выбор. И так далее. Итак, для любого выбора радиуса р, точки (r, -r) а также (-r, r) не должен быть выбран. Кроме этого, ваш алгоритм выбора должен быть таким же, как и у прямоугольной сетки.
Просто убедитесь, что ваша ось правильно настроена на гексагональной сетке, и что вы соответствующим образом нумеруете свои плитки.
Реализация
Давайте расширим это немного. Теперь мы знаем, что движение вдоль любого направления в сетке стоит нам 1. И движение вдоль растянуты Направление стоит нам 2. Смотрите (0, 0) в (-1, 1) например.
Зная это, мы можем вычислить кратчайшее расстояние между любыми двумя плитками на такой сетке, разложив расстояние на две составляющие: диагональное движение и прямое движение вдоль одной из осей.
Например, для расстояния между (1, 1) а также (-2, 5) на нормальной сетке имеем:
Normal distance = (1, 1) - (-2, 5) = (3, -4)
Это был бы вектор расстояния между двумя плитками, если бы они были на квадратной сетке. Однако нам нужно компенсировать деформацию сетки, поэтому мы разлагаемся следующим образом:
(3, -4) = (3, -3) + (0, -1)
Как видите, мы разложили вектор на один диагональный (3, -3) и один прямой вдоль оси (0, -1),
Теперь мы проверим, находится ли диагональ вдоль оси деформации, которая является любой точкой (n, -n) где n целое число, которое может быть как положительным, так и отрицательным.
(3, -3) действительно удовлетворяет этому условию, так что этот диагональный вектор вдоль деформации. Это означает, что длина (или стоимость) этого вектора вместо 3, это будет двойной, то есть 6,
Итак, подведем итоги. Расстояние между (1, 1) а также (-2, 5) длина (3, -3) плюс длина (0, -1), То есть distance = 3 * 2 + 1 = 7,
Реализация в C ++
Ниже приведена реализация в C ++ алгоритма, который я объяснил выше:
int ComputeDistanceHexGrid(const Point & A, const Point & B)
{
// compute distance as we would on a normal grid
Point distance;
distance.x = A.x - B.x;
distance.y = A.y - B.y;
// compensate for grid deformation
// grid is stretched along (-n, n) line so points along that line have
// a distance of 2 between them instead of 1
// to calculate the shortest path, we decompose it into one diagonal movement(shortcut)
// and one straight movement along an axis
Point diagonalMovement;
int lesserCoord = abs(distance.x) < abs(distance.y) ? abs(distance.x) : abs(distance.y);
diagonalMovement.x = (distance.x < 0) ? -lesserCoord : lesserCoord; // keep the sign
diagonalMovement.y = (distance.y < 0) ? -lesserCoord : lesserCoord; // keep the sign
Point straightMovement;
// one of x or y should always be 0 because we are calculating a straight
// line along one of the axis
straightMovement.x = distance.x - diagonalMovement.x;
straightMovement.y = distance.y - diagonalMovement.y;
// calculate distance
size_t straightDistance = abs(straightMovement.x) + abs(straightMovement.y);
size_t diagonalDistance = abs(diagonalMovement.x);
// if we are traveling diagonally along the stretch deformation we double
// the diagonal distance
if ( (diagonalMovement.x < 0 && diagonalMovement.y > 0) ||
(diagonalMovement.x > 0 && diagonalMovement.y < 0) )
{
diagonalDistance *= 2;
}
return straightDistance + diagonalDistance;
}
Теперь, учитывая вышеизложенное, реализовано ComputeDistanceHexGrid функция, теперь вы можете иметь наивную, неоптимизированную реализацию алгоритма выбора, которая будет игнорировать любые плитки дальше указанного диапазона выбора:
int _tmain(int argc, _TCHAR* argv[])
{
// your radius selection now becomes your usual orthogonal algorithm
// except you eliminate hex tiles too far away from your selection center
// for(x-range;x+range;x++); for(y-range;y+range;y++);
Point selectionCenter = {1, 1};
int range = 1;
for ( int x = selectionCenter.x - range;
x <= selectionCenter.x + range;
++x )
{
for ( int y = selectionCenter.y - range;
y <= selectionCenter.y + range;
++y )
{
Point p = {x, y};
if ( ComputeDistanceHexGrid(selectionCenter, p) <= range )
cout << "(" << x << ", " << y << ")" << endl;
else
{
// do nothing, skip this tile since it is out of selection range
}
}
}
return 0;
}
Для выбора точки (1, 1) и ряд 1вышеуказанный код будет отображать ожидаемый результат:
(0, 0)
(0, 1)
(1, 0)
(1, 1)
(1, 2)
(2, 1)
(2, 2)
Возможная оптимизация
Чтобы оптимизировать это, вы можете включить логику знания того, как далеко плитка находится от точки выбора (логика найдена в ComputeDistanceHexGrid) непосредственно в ваш цикл выбора, чтобы вы могли выполнять итерацию сетки таким образом, чтобы вообще избежать выхода за пределы диапазона.
Другие решения
Просто расположите вашу сетку следующим образом:
+-----+-----+-----+-----+
| 0 | 1 | 2 | 3 | even row
+-----+-----+-----+--+-----+
| 4 | 5 | 6 | 7 | ==> odd row
+--+-----+-----+-----+--+--+
| 8 | 9 | 10 | 11 | even row
+-----+-----+-----+-----+
Для нечетных рядов (N>>2)&1 == 1нужно концептуально сместить слоты на половину ширины слота.
Тогда соседями являются {N-1, N + 1, N-a, N-a + 1, N + b, N + b + 1}, a = b = 4.
Для четных строк a = 5, b = 3. (а = выше, б = ниже)
С этой идеей можно построить список смежности и выполнить поиск в ширину (с некоторыми метриками для расстояния — евклидово или любым другим манхэттенским расстоянием, которое будет называться на медовой сетке).
