Между вращением

У меня есть изображение (скажем, это простой прямоугольник), расположенное слева от моего экрана, которое я могу перемещать вверх и вниз. При перемещении вверх я использую некоторую простую тригонометрию, чтобы повернуть его так, чтобы прямоугольник «указывал» на верхний правый угол экрана. При движении вниз он указывает на левый нижний угол экрана.

Учитывая, что мое приложение использует следующую систему координат:

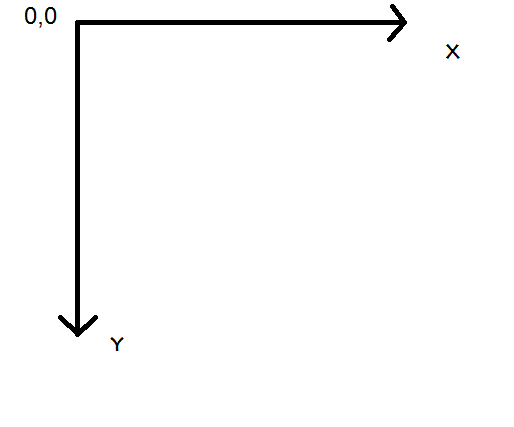
Я использую следующий код для достижения поворота:

// moving upwards
rotation = -atan2(position.y , res.x - position.x));

// moving downwards
rotation = atan2(res.y - position.y , res.x - position.x));

где res является контрольной точкой и position это позиция (верхний левый угол) нашего прямоугольного изображения. (Для информации о atan2(): atan2 () на cplusplus.com).

Это работает очень хорошо: он вращается больше, когда дальше от контрольной точки (res). Однако, скажем, изображение находится внизу экрана. Если мы переместим его вверх, он очень внезапно начнет вращаться. Я хотел бы «вставить» это вращение, чтобы оно было сглажено.

Что я имею в виду, внезапно вращаясь, это:
Допустим, прямоугольник не движется в кадре n, поэтому его вращение составляет 0 градусов. Затем я нажимаю стрелку вверх, чтобы вычислить угол. В кадре n + 1 угол составляет 30 градусов (например). Это конечно не очень гладко.

Мой вопрос понятен? Как мне это сделать?