Метод оптимизации для определения плавающего статуса объекта

Задача, которую необходимо решить, — найти плавающее состояние плавающего тела, учитывая его вес и центр тяжести.

Функция, которую я использую, вычисляет смещенный объем и центр движения тела с учетом утопления, пятки и отделки.
Где утолщение является единицей длины, а пятка / отделка — это угол, ограниченный значением от -90 до 90.

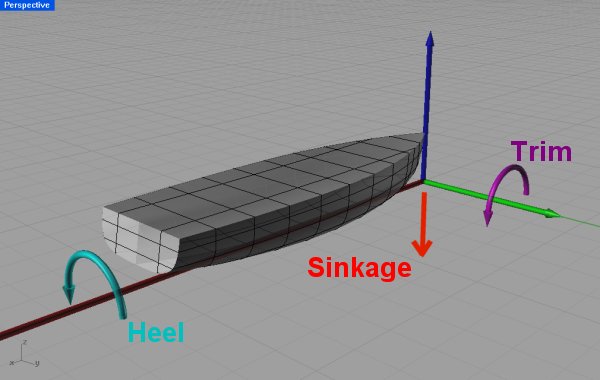
Плавающий статус обнаруживается, когда смещенный объем равен весу, а центр тяжести находится на вертикальной линии с центром движения.

Я реализовал это как нелинейную задачу нахождения корня Ньютона-Рафсона с 3-мя переменными (сток, триммер, пятка) и 3 уравнениями.
Этот метод работает, но требует хороших начальных догадок. Поэтому я надеюсь найти либо лучший подход для этого, либо хороший метод для определения начальных значений.

Ниже приведен код алгоритма Ньютона и Якобиана, используемый для итерации Ньютона-Рафсона. Функция громкости принимает параметры грузоподъемности, пятки и отделки. И возвращает объем, и координаты центра города.

Я также включил алгоритмы maxabs и GSolve2, я полагаю, что они взяты из Numeric Recipies.

void jacobian(float x[], float weight, float vcg, float tcg, float lcg, float jac[][3], float f0[]) {
float h = 0.0001f;
float temp;
float j_volume, j_vcb, j_lcb, j_tcb;
float f1[3];

volume(x[0], x[1], x[2], j_volume, j_lcb, j_vcb, j_tcb);
f0[0] = j_volume-weight;
f0[1] = j_tcb-tcg;
f0[2] = j_lcb-lcg;

for (int i=0;i<3;i++) {
temp = x[i];
x[i] = temp + h;
volume(x[0], x[1], x[2], j_volume, j_lcb, j_vcb, j_tcb);

f1[0] = j_volume-weight;
f1[1] = j_tcb-tcg;
f1[2] = j_lcb-lcg;
x[i] = temp;

jac[0][i] = (f1[0]-f0[0])/h;
jac[1][i] = (f1[1]-f0[1])/h;
jac[2][i] = (f1[2]-f0[2])/h;
}
}void newton(float weight, float vcg, float tcg, float lcg, float &sinkage, float &heel, float &trim) {
float x[3] = {10,1,1};

float accuracy = 0.000001f;
int ntryes = 30;
int i = 0;
float jac[3][3];
float max;
float f0[3];
float gauss_f0[3];

while (i < ntryes) {
jacobian(x, weight, vcg, tcg, lcg, jac, f0);

if (sqrt((f0[0]*f0[0]+f0[1]*f0[1]+f0[2]*f0[2])/2) < accuracy) {
break;
}

gauss_f0[0] = -f0[0];
gauss_f0[1] = -f0[1];
gauss_f0[2] = -f0[2];

GSolve2(jac, 3, gauss_f0);

x[0] = x[0]+gauss_f0[0];
x[1] = x[1]+gauss_f0[1];
x[2] = x[2]+gauss_f0[2];

// absmax(x) - Return absolute max value from an array
max = absmax(x);
if (max < 1) max = 1;

if (sqrt((gauss_f0[0]*gauss_f0[0]+gauss_f0[1]*gauss_f0[1]+gauss_f0[2]*gauss_f0[2])) < accuracy*max) {
x[0]=x2[0];
x[1]=x2[1];
x[2]=x2[2];
break;
}

i++;
}

sinkage = x[0];
heel = x[1];
trim = x[2];
}

int GSolve2(float a[][3],int n,float b[]) {
float x,sum,max,temp;
int i,j,k,p,m,pos;

int nn = n-1;

for (k=0;k<=n-1;k++)
{
/* pivot*/
max=fabs(a[k][k]);
pos=k;for (p=k;p<n;p++){
if (max < fabs(a[p][k])){
max=fabs(a[p][k]);
pos=p;
}
}

if (ABS(a[k][pos]) < EPS) {
writeLog("Matrix is singular");
break;
}

if (pos != k) {
for(m=k;m<n;m++){
temp=a[pos][m];
a[pos][m]=a[k][m];
a[k][m]=temp;
}
}

/*   convert to upper triangular form */
if ( fabs(a[k][k])>=1.e-6)
{
for (i=k+1;i<n;i++)
{
x = a[i][k]/a[k][k];
for (j=k+1;j<n;j++) a[i][j] = a[i][j] -a[k][j]*x;
b[i] = b[i] - b[k]*x;
}
}
else
{
writeLog("zero pivot found in line:%d",k);
return 0;
}
}

/*   back substitution */
b[nn] = b[nn] / a[nn][nn];
for (i=n-2;i>=0;i--)
{
sum = b[i];
for (j=i+1;j<n;j++)
sum = sum - a[i][j]*b[j];
b[i] = sum/a[i][i];
}
return 0;
}

float absmax(float x[]) {
int i = 1;
int n = sizeof(x);
float max = x[0];
while (i < n) {
if (max < x[i]) {
max = x[i];
}
i++;
}
return max;
}