Метаэвристический тасование
В настоящее время я работаю над NP-полной проблемой и для этой цели внедрил персональный генетический алгоритм. Результаты больше, чем я мог ожидать. Я думаю, что с хорошо разработанной функцией фитнеса и тщательно настроенной популяцией / мутацией пары GA в некоторых случаях может быть отличным инструментом.
Во всяком случае, сейчас я ищу метаэвристику (GA, имитируемый отжиг …), способную производить оптимальную перетасовку.
В этом контексте я имею в виду непредвзятыйа ля Фишер-Йейтс) случайная перестановка конечного множества. Как колода карт. Огромный (~ 500! Перестановок).
Значения этого набора все разные. Никаких столкновений не ожидается.
Из-за этого противоречия у меня есть некоторые трудности для реализации решения GA. Действительно, перемешанные значения не могут быть использованы в качестве генов. Легко понять, почему:
#include <iostream>
#include <vector>
#define SPLICING 50 // 50|50 one-point crossover
int crossover(int gene, int DNA_length, int A, int B)
{if (gene < (SPLICING*DNA_length)/100) return A; else return B;}
int main() {
std::vector<int> A, B, C;
A = { 3, 4, 8, 12, 2, 0, 9, 7, 10, 20 };
B = { 8, 10, 3, 4, 20, 0, 7, 9, 2, 12 };
int DNA_length = int(A.size());
for (int i=0; i<DNA_length; i++) {
C.push_back(crossover(i, DNA_length, A[i], B[i]));
if (i == DNA_length/2) std::cout << "| ";
std::cout << C[i] << " ";}
}
Выход: 3 4 8 12 2 | 0 7 9 2 12
Есть два столкновения (2, 12).
Мой ожидаемый результат примерно такой: 3 4 8 12 2 | 0 7 9 10 20 (без столкновений, идеальное перемешивание оригинального набора).
Затем мне нужно закодировать порядок этих значений, чтобы избежать подобных трудностей.
Наивный способ — идентифицировать каждое значение уникальным ключом. Но созданный тогда набор является порядковый один, потому что это относится к последовательности значений.
Мне кажется, что функция кроссовера имеет дело с ordinality из ДНК родителей. Но я не могу обернуть голову вопросом смешивания двух нелинейно упорядоченных порядковых подмножеств (родительских срезов ДНК) порядкового набора (целой ДНК) без столкновения!
Может быть, я могу полагаться только на мутацию для конвергенции. Нет выбора, нет родителей / детей, и только функция обмена в том же наборе (ДНК человека). Короче говоря: не очень убедительно.
Действительно легко переставлять порядковые числа в уникальном конечном множестве (например, тривиально: первое становится седьмым, второе, десятым и т. Д.). Но я не уверен, имеет ли смысл говорить, что первый из набора А становится седьмым, когда второй из набора B становится десятой частью нового набора.
Тогда мой вопрос:
По вашему мнению, можно ли перетасовать ординальность множества с помощью функции кроссовера в контексте генетического алгоритма? Если нет, можете ли вы предложить метаэвристический подход, более эффективный для этой цели, чем метод грубой силы, восхождения на гору или генетический алгоритм?
Спасибо.
Решение
То, что вы ищете, называется генетическими алгоритмами, основанными на порядке. У вас есть много операторов пересечения и мутации на основе порядка, которые предназначены для работы с такой проблемой. Самый простой оператор кроссовера работает следующим образом:
- Выберите точки пересечения
- Скопируйте деталь из parent1 в точках пересечения на первого сына.
- Составьте список элементов parent1, которые находятся вне точек пересечения
- Расположите элементы неиспользуемого списка в том же порядке, что и в parent2
- Скопируйте эти элементы первому сыну в порядке, установленном на шаге 4.
Вы можете увидеть пример из моей книги на рисунке ниже (извините, но описания на португальском языке — пожалуйста, сопоставьте со списком выше):
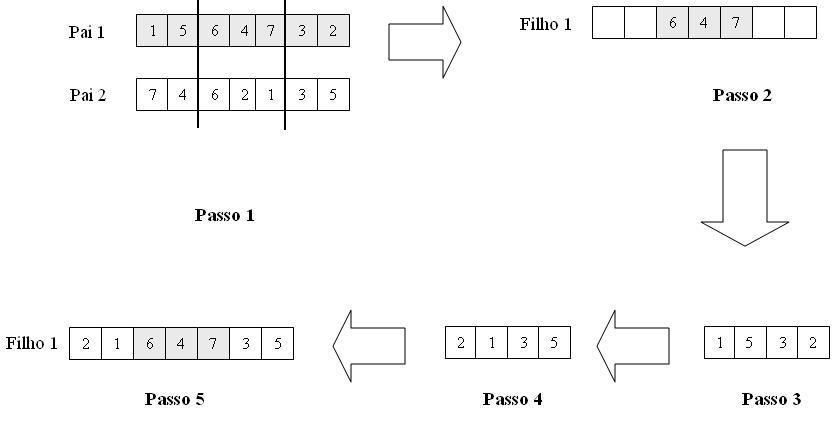
Вы можете искать в сети операторов, основанных на заказе, или, если хотите, проверить цифры из моей книги на Книга «Мой генетический алгоритм». Интересующие вас цифры приведены в главе 10 (вы можете использовать переводчик Google, чтобы понять легенды).
Вам не нужно иметь в виду, что в книге используются последовательные числа — если у вас нет повторений, все объясненные концепции верны для вашей проблемы.
Я надеюсь, что это помогает.
Другие решения
