математика — Найти расстояние между трехмерной точкой и ориентированным эллипсом в трехмерном пространстве (C ++)
Чтобы дать некоторое представление об этом вопросе, я создаю игру, которая должна знать, находится ли «Орбита» объекта в пределах допуска другой Орбиты. Чтобы показать это, я строю форму тора с заданным радиусом (допуском), используя целевую орбиту, и теперь мне нужно проверить, находится ли эллипс внутри этого тора.
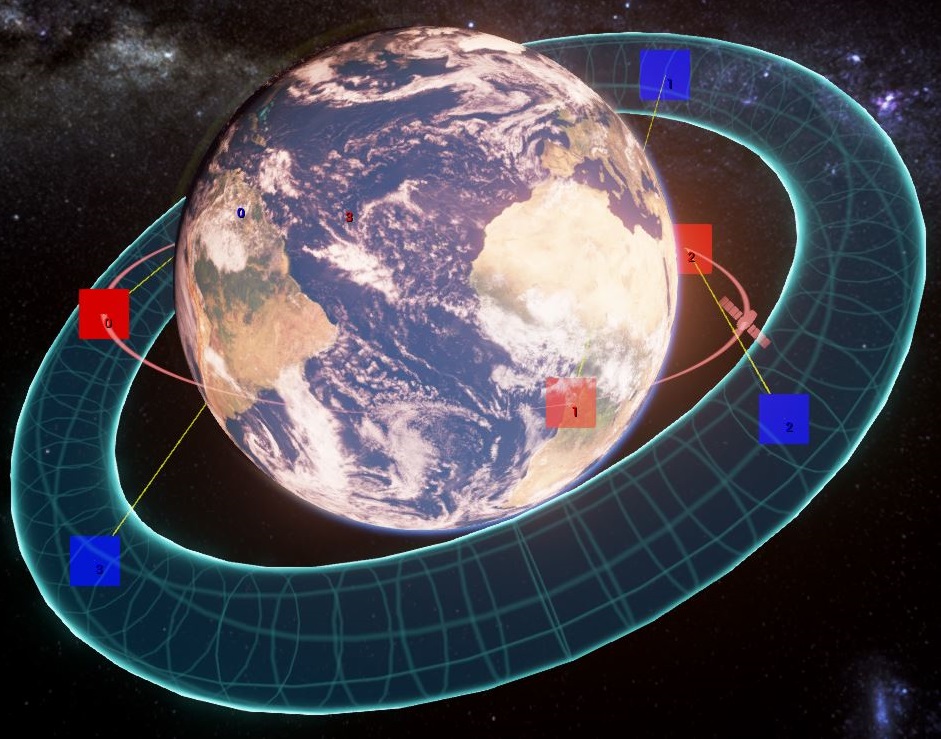
Я заблудился в уравнениях по обмену Math / Stack, поэтому прошу более конкретное решение. Для ясности, вот изображение игры с Тором и Орбитой (красная линия). Проще говоря, я хочу проверить, находится ли эта красная орбита в пределах этой формы Тора.
Я считаю, что мне нужно сделать четыре точки в World-Space на одной из этих орбит (достаточно легко сделать). Затем мне нужно вычислить кратчайшее расстояние между этой точкой и эллипсом других орбит. Это сложная часть. Существует несколько примеров нахождения кратчайшего расстояния от точки до эллипса, но все они двумерные, и им довольно трудно следовать.
Если это расстояние будет меньше, чем допуск для всех четырех точек, то подумайте, что это означает, что орбита находится внутри целевого тора.
Для простоты, источник всех этих орбит всегда находится в мире Origin (0, 0, 0) — и моя система координат Z-Up. У каждой орбиты есть ряд параметров, которые ее определяют (элементы орбиты).
Решение
Здесь простой подход:
-
Пример каждой орбиты для набора
Nточки.Пусть точки с первой орбиты будут
Aи со второй орбитыB,const int N=36; float A[N][3],B[N][3]; -
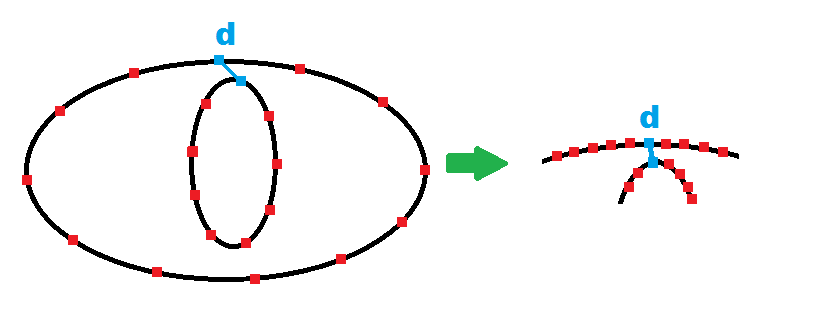
найти 2 ближайших точек
так
d=|A[i]-B[i]|минимален Еслиdменьше или равен вашему краю / порогу, тогда орбиты находятся слишком близко друг к другу. -
скорость против точности
Если вы не используете какой-то продвинутый метод для # 2 тогда его вычисление будет
O(N^2)что немного страшно Чем большеNлучшая точность результата, но гораздо больше времени для вычислений. Есть способы, как исправить оба. Например:
Другие решения
Я думаю, что у меня может быть новое решение.
- Построить четыре точки на текущей орбите (эллипс).
- Спроецируйте эти точки на плоскость целевой орбиты (тор).
- Используя наклон целевой орбиты в качестве нормали к плоскости, рассчитайте угол между каждой (нормализованной) точкой и аргументом периапазиса
на целевой орбите. - Используйте этот угол в качестве средней аномалии и вычислите эквивалентную эксцентрическую аномалию.
- Используйте эти эксцентричные аномалии для построения четырех точек на целевой орбите, которые должны быть ближайшими к другой орбите.
- Проверьте расстояние между этими точками.
Трудность здесь заключается в вычислении угла и преобразовании его в аномалию на другой орбите. Это должно быть точнее и быстрее, чем рекурсивная функция. Буду обновлять, когда я попробую это.
РЕДАКТИРОВАТЬ:
Да, это работает!
// The Four Locations we will use for the checks
TArray<FVector> CurrentOrbit_CheckPositions;
TArray<FVector> TargetOrbit_ProjectedPositions;
CurrentOrbit_CheckPositions.SetNum(4);
TargetOrbit_ProjectedPositions.SetNum(4);
// We first work out the plane of the target orbit.
const FVector Target_LANVector = FVector::ForwardVector.RotateAngleAxis(TargetOrbit.LongitudeAscendingNode, FVector::UpVector); // Vector pointing to Longitude of Ascending Node
const FVector Target_INCVector = FVector::UpVector.RotateAngleAxis(TargetOrbit.Inclination, Target_LANVector); // Vector pointing up the inclination axis (orbit normal)
const FVector Target_AOPVector = Target_LANVector.RotateAngleAxis(TargetOrbit.ArgumentOfPeriapsis, Target_INCVector); // Vector pointing towards the periapse (closest approach)
// Geometric plane of the orbit, using the inclination vector as the normal.
const FPlane ProjectionPlane = FPlane(Target_INCVector, 0.f); // Plane of the orbit. We only need the 'normal', and the plane origin is the Earths core (periapse focal point)
// Plot four points on the current orbit, using an equally-divided eccentric anomaly.
const float ECCAngle = PI / 2.f;
for (int32 i = 0; i < 4; i++)
{
// Plot the point, then project it onto the plane
CurrentOrbit_CheckPositions[i] = PosFromEccAnomaly(i * ECCAngle, CurrentOrbit);
CurrentOrbit_CheckPositions[i] = FVector::PointPlaneProject(CurrentOrbit_CheckPositions[i], ProjectionPlane);
// TODO: Distance from the plane is the 'Depth'. If the Depth is > Acceptance Radius, we are outside the torus and can early-out here
// Normalize the point to find it's direction in world-space (origin in our case is always 0,0,0)
const FVector PositionDirectionWS = CurrentOrbit_CheckPositions[i].GetSafeNormal();
// Using the Inclination as the comparison plane - find the angle between the direction of this vector, and the Argument of Periapse vector of the Target orbit
// TODO: we can probably compute this angle once, using the Periapse vectors from each orbit, and just multiply it by the Index 'I'
float Angle = FMath::Acos(FVector::DotProduct(PositionDirectionWS, Target_AOPVector));
// Compute the 'Sign' of the Angle (-180.f - 180.f), using the Cross Product
const FVector Cross = FVector::CrossProduct(PositionDirectionWS, Target_AOPVector);
if (FVector::DotProduct(Cross, Target_INCVector) > 0)
{
Angle = -Angle;
}
// Using the angle directly will give us the position at th eccentric anomaly. We want to take advantage of the Mean Anomaly, and use it as the ecc anomaly
// We can use this to plot a point on the target orbit, as if it was the eccentric anomaly.
Angle = Angle - TargetOrbit.Eccentricity * FMathD::Sin(Angle);
TargetOrbit_ProjectedPositions[i] = PosFromEccAnomaly(Angle, TargetOrbit);}
Я надеюсь, что комментарии описывают, как это работает. Окончательно решен после нескольких месяцев царапин на голове. Спасибо всем!