математика — C ++ программа, которая вычисляет ln для заданной переменной x без использования готовых функций
Я искал уравнение, которое вычисляет ln числа x и обнаружил, что это уравнение:
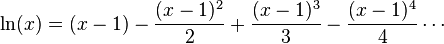
и я написал этот код для его реализации:
double ln = x-1 ;
for(int i=2;i<=5;i++)
{
double tmp = 1 ;
for(int j=1;j<=i;j++)
tmp *= (x-1) ;
if(i%2==0)
ln -= (tmp/i) ;
else
ln += (tmp/i) ;
}
cout << "ln: " << setprecision(10) << ln << endl ;
но, к сожалению, я получаю результаты, совершенно отличные от результатов на калькуляторе, особенно для больших чисел, кто-нибудь может сказать мне, где проблема?
Решение
Уравнение, на которое вы ссылаетесь, представляет собой бесконечный ряд, подразумеваемый многоточием, следующим за основной частью уравнения, и как более четко указано в предыдущей формулировке на той же странице:
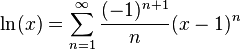
В вашем случае вы рассчитываете только первые четыре условия. Более поздние условия добавят небольшие уточнения к результату, чтобы приблизиться к фактическому значению, но в конечном итоге для вычисления всех бесконечных шагов потребуется бесконечное время.
Однако, что вы можете сделать, это приблизительный ваш ответ на что-то вроде:
double ln(double x) {
// validate 0 < x < 2
double threshold = 1e-5; // set this to whatever threshold you want
double base = x-1; // Base of the numerator; exponent will be explicit
int den = 1; // Denominator of the nth term
int sign = 1; // Used to swap the sign of each term
double term = base; // First term
double prev = 0; // Previous sum
double result = term; // Kick it off
while (fabs(prev - result) > threshold) {
den++;
sign *=- 1;
term *= base;
prev = result;
result += sign * term / den;
}
return result;
}
Осторожно: я на самом деле не проверял это, поэтому может потребоваться некоторая настройка.
Это вычисляет каждый член до тех пор, пока абсолютная разница между двумя последовательными членами не станет меньше установленного вами порогового значения.
Теперь это не очень эффективный способ сделать это. Лучше работать с функциями языка, который вы используете (в данном случае C ++), для вычисления естественного журнала (который, как я полагаю, уже есть у другого автора). Но, возможно, стоит попробовать это для себя, чтобы увидеть, как это работает.
Кроме того, как отмечает Барак Манос ниже, эта серия Тейлора сходится только в диапазоне (0, 2), поэтому вам нужно будет проверить значение x лежит в этом диапазоне, прежде чем пытаться запустить фактические вычисления.
Другие решения
Я считаю, что естественный журнал на языке C ++ — это просто журнал
Не мешало бы пользоваться long а также long double вместо int а также double, Это может получить немного больше точности для некоторых больших значений. Кроме того, ваша серия, простирающаяся всего на 5 уровней, также ограничивает вашу точность.
Использование такой серии в основном является приближением логарифмического ответа.
Эта версия должна быть несколько быстрее:
double const scale = 1.5390959186233239e-16;
double const offset = -709.05401552996614;
double fast_ln(double x)
{
uint64_t xbits;
memcpy(&xbits, &x, 8);
// if memcpy not allowed, use
// for( i = 0; i < 8; ++i ) i[(char*)xbits] = i[(char*)x];
return xbits * scale + offset;
}
Хитрость заключается в том, что здесь используется 64-разрядное целое число * 64-разрядное умножение с плавающей точкой, которое включает преобразование целого числа в число с плавающей запятой. Упомянутое представление с плавающей точкой похоже на научную нотацию и требует логарифма, чтобы найти соответствующий показатель степени … но это делается чисто аппаратно и очень быстро.
Однако в каждой октаве выполняется линейное приближение, что не очень точно. Использование таблицы поиска для этих битов было бы намного лучше.
Эта формула не будет работать для больших входных данных, потому что она потребовала бы, чтобы вы приняли во внимание член наивысшей степени, который вы не можете, потому что их бесконечно много.
Это будет работать только для небольших входных данных, где важны только первые термины вашей серии.
Вы можете найти способы сделать это здесь: Http: //en.wikipedia.or/wiki/Pollard%27s_rho_algorithm_for_logarithms
