маршрутизация вектора расстояний с использованием алгоритма Беллмана Форда для матрицы затрат неориентированного графа
Я пытаюсь реализовать алгоритм векторного расстояния, используя алгоритм Беллмана Форда для ориентированного графа. Мой вход — это исходная матрица, которая описывает вес узлов, смежных с другими узлами. Чтобы рассчитать кратчайший путь между узлами, мне также нужно рассчитать итерации, которые произойдут с изменениями в матрице. Как рассчитать итерации, после которых матрица даст кратчайший путь для всех узлов?
Пример исходной матрицы узлов приведен ниже, мы рассматриваем график как
R1 -> R2 = 3
R1 -> R3 = 999
R1 -> R4 = 7
R2 -> R3 = 6
R2 -> R4 = 999
R3 -> R4 = 2
Здесь 999 рассматривается как бесконечность, так как узлы не связаны напрямую.
Решение
Это похоже на то, что вы должны быть в состоянии извлечь из алгоритм. AFAICS, матрица будет заполнена результатом после того, как в основном 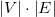 итераций.
итераций.
Другие решения
