Марширующие кубики

http://en.wikipedia.org/wiki/Marching_cubes

http://en.wikipedia.org/wiki/Marching_cubes#External_links

Пол Бурк «Обзор и исходный код».

http://paulbourke.net/geometry/polygonise/

Qt_MARCHING_CUBES.zip: пример Qt / OpenGL любезно предоставлен доктором Клаусом Мильтенбергером.

http://paulbourke.net/geometry/polygonise/Qt_MARCHING_CUBES.zip

Пример требует повышения, но похоже, что он, вероятно, должен работать.

В его примере это имеет в marchingcubes.cppНесколько разных методов расчета марширующих кубов: vMarchCube1 а также vMarchCube2,

В комментариях говорится vMarchCube2 выполняет алгоритм Марширующих тетраэдров для одного куба, выполнив шесть вызовов vMarchTetrahedron.

Ниже приведен источник для первого vMarchCube1:

//vMarchCube1 performs the Marching Cubes algorithm on a single cube
GLvoid GL_Widget::vMarchCube1(const GLfloat &fX, const GLfloat &fY, const GLfloat &fZ, const GLfloat &fScale, const GLfloat &fTv)
{
GLint iCorner, iVertex, iVertexTest, iEdge, iTriangle, iFlagIndex, iEdgeFlags;
GLfloat fOffset;
GLvector sColor;
GLfloat afCubeValue[8];
GLvector asEdgeVertex[12];
GLvector asEdgeNorm[12];

//Make a local copy of the values at the cube's corners
for(iVertex = 0; iVertex < 8; iVertex++)
{
afCubeValue[iVertex] = (this->*fSample)(fX + a2fVertexOffset[iVertex][0]*fScale,fY + a2fVertexOffset[iVertex][1]*fScale,fZ + a2fVertexOffset[iVertex][2]*fScale);
}

//Find which vertices are inside of the surface and which are outside
iFlagIndex = 0;
for(iVertexTest = 0; iVertexTest < 8; iVertexTest++)
{
if(afCubeValue[iVertexTest] <= fTv)     iFlagIndex |= 1<<iVertexTest;
}

//Find which edges are intersected by the surface
iEdgeFlags = aiCubeEdgeFlags[iFlagIndex];

//If the cube is entirely inside or outside of the surface, then there will be no intersections
if(iEdgeFlags == 0)
{
return;
}

//Find the point of intersection of the surface with each edge
//Then find the normal to the surface at those points
for(iEdge = 0; iEdge < 12; iEdge++)
{
//if there is an intersection on this edge
if(iEdgeFlags & (1<<iEdge))
{
fOffset = fGetOffset(afCubeValue[ a2iEdgeConnection[iEdge][0] ],afCubeValue[ a2iEdgeConnection[iEdge][1] ], fTv);

asEdgeVertex[iEdge].fX = fX + (a2fVertexOffset[ a2iEdgeConnection[iEdge][0] ][0]  +  fOffset * a2fEdgeDirection[iEdge][0]) * fScale;
asEdgeVertex[iEdge].fY = fY + (a2fVertexOffset[ a2iEdgeConnection[iEdge][0] ][1]  +  fOffset * a2fEdgeDirection[iEdge][1]) * fScale;
asEdgeVertex[iEdge].fZ = fZ + (a2fVertexOffset[ a2iEdgeConnection[iEdge][0] ][2]  +  fOffset * a2fEdgeDirection[iEdge][2]) * fScale;

vGetNormal(asEdgeNorm[iEdge], asEdgeVertex[iEdge].fX, asEdgeVertex[iEdge].fY, asEdgeVertex[iEdge].fZ);
}
}//Draw the triangles that were found.  There can be up to five per cube
for(iTriangle = 0; iTriangle < 5; iTriangle++)
{
if(a2iTriangleConnectionTable[iFlagIndex][3*iTriangle] < 0) break;

for(iCorner = 0; iCorner < 3; iCorner++)
{
iVertex = a2iTriangleConnectionTable[iFlagIndex][3*iTriangle+iCorner];

vGetColor(sColor, asEdgeVertex[iVertex], asEdgeNorm[iVertex]);
glColor4f(sColor.fX, sColor.fY, sColor.fZ, 0.6);
glNormal3f(asEdgeNorm[iVertex].fX,   asEdgeNorm[iVertex].fY,   asEdgeNorm[iVertex].fZ);
glVertex3f(asEdgeVertex[iVertex].fX, asEdgeVertex[iVertex].fY, asEdgeVertex[iVertex].fZ);
}
}
}

ОБНОВЛЕНИЕ: Github рабочий пример, проверено

https://github.com/peteristhegreat/qt-marching-cubes

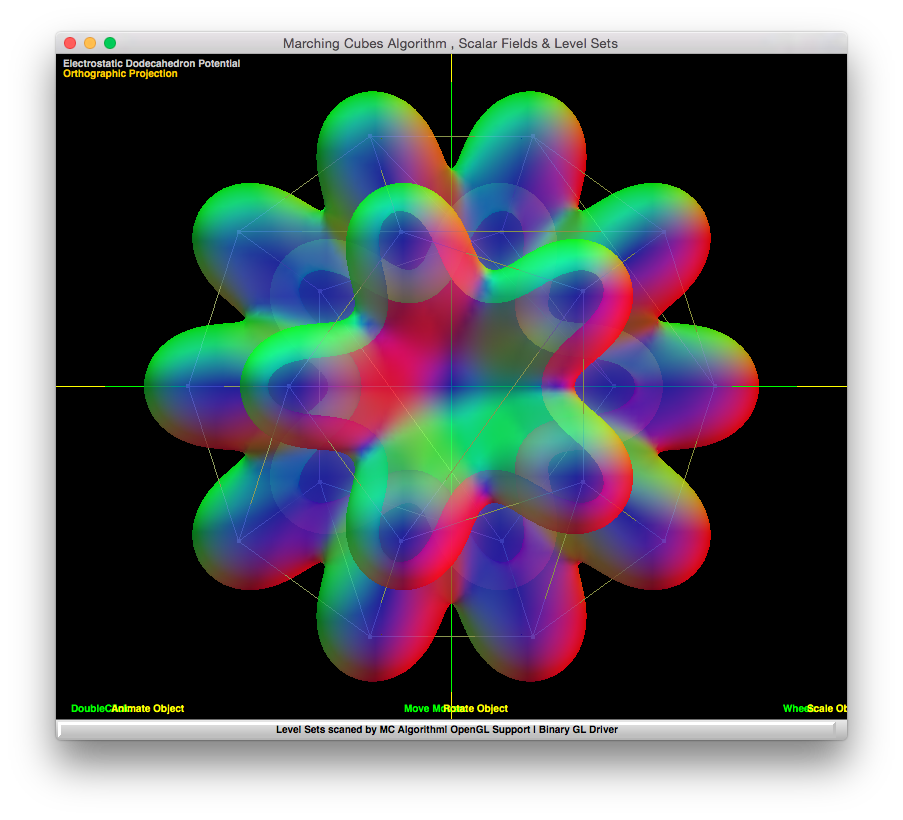
Надеюсь, это поможет.