Логистическая регрессия для обнаружения неисправностей в изображении

По сути, я хочу обнаружить ошибку в изображении, используя логистическую регрессию. Я надеюсь получить такой отзыв о моем подходе, который заключается в следующем:

Для тренировки:

1. Возьмите небольшой фрагмент изображения с пометкой «плохо» и «хорошо»
2. Оттенки серого, затем разбейте их на ряд сегментов 5 * 5 пикселей
3. Рассчитать гистограмму интенсивности пикселей для каждого из этих сегментов
4. Передайте гистограммы вместе с метками в класс логистической регрессии для обучения
5. Разбейте все изображение на 5 * 5 сегментов и прогнозируйте «хорошо» / «плохо» для каждого сегмента.

Используя функцию sigmod, уравнение линейной регрессии имеет вид:

1/ (1 - e^(xθ))

Где х — входные значения, а тета (θ) — веса. Я использую градиентный спуск для обучения сети. Мой код для этого:

void LogisticRegression::Train(float **trainingSet,float *labels, int m)
{
float tempThetaValues[m_NumberOfWeights];

for (int iteration = 0; iteration < 10000; ++iteration)
{
// Reset the temp values for theta.
memset(tempThetaValues,0,m_NumberOfWeights*sizeof(float));

float error = 0.0f;

// For each training set in the example
for (int trainingExample = 0; trainingExample < m; ++trainingExample)
{
float * x = trainingSet[trainingExample];
float y = labels[trainingExample];

// Partial derivative of the cost function.
float h = Hypothesis(x) - y;
for (int i =0; i < m_NumberOfWeights; ++i)
{
tempThetaValues[i] += h*x[i];
}
float cost = h-y; //Actual J(theta), Cost(x,y), keeps giving NaN use MSE for now
error += cost*cost;
}

// Update the weights using batch gradient desent.
for (int theta = 0; theta < m_NumberOfWeights; ++theta)
{
m_pWeights[theta] = m_pWeights[theta] - 0.1f*tempThetaValues[theta];
}

printf("Cost on iteration[%d] = %f\n",iteration,error);
}
}

Где сигмоид и гипотеза рассчитываются с использованием:

float LogisticRegression::Sigmoid(float z) const
{
return 1.0f/(1.0f+exp(-z));
}

float LogisticRegression::Hypothesis(float *x) const
{
float z = 0.0f;
for (int index = 0; index < m_NumberOfWeights; ++index)
{
z += m_pWeights[index]*x[index];
}
return Sigmoid(z);
}

И окончательный прогноз дает:

int LogisticRegression::Predict(float *x)
{
return Hypothesis(x) > 0.5f;
}

Поскольку мы используем гистограмму интенсивностей, входные и весовые массивы составляют 255 элементов. Я надеюсь использовать его на изображении яблока с синяком и идентифицировать поврежденные части. (Нормализованные) гистограммы для всех тренировочных наборов brused и apple выглядят примерно так:

Для «хороших» участков яблока (у = 0):

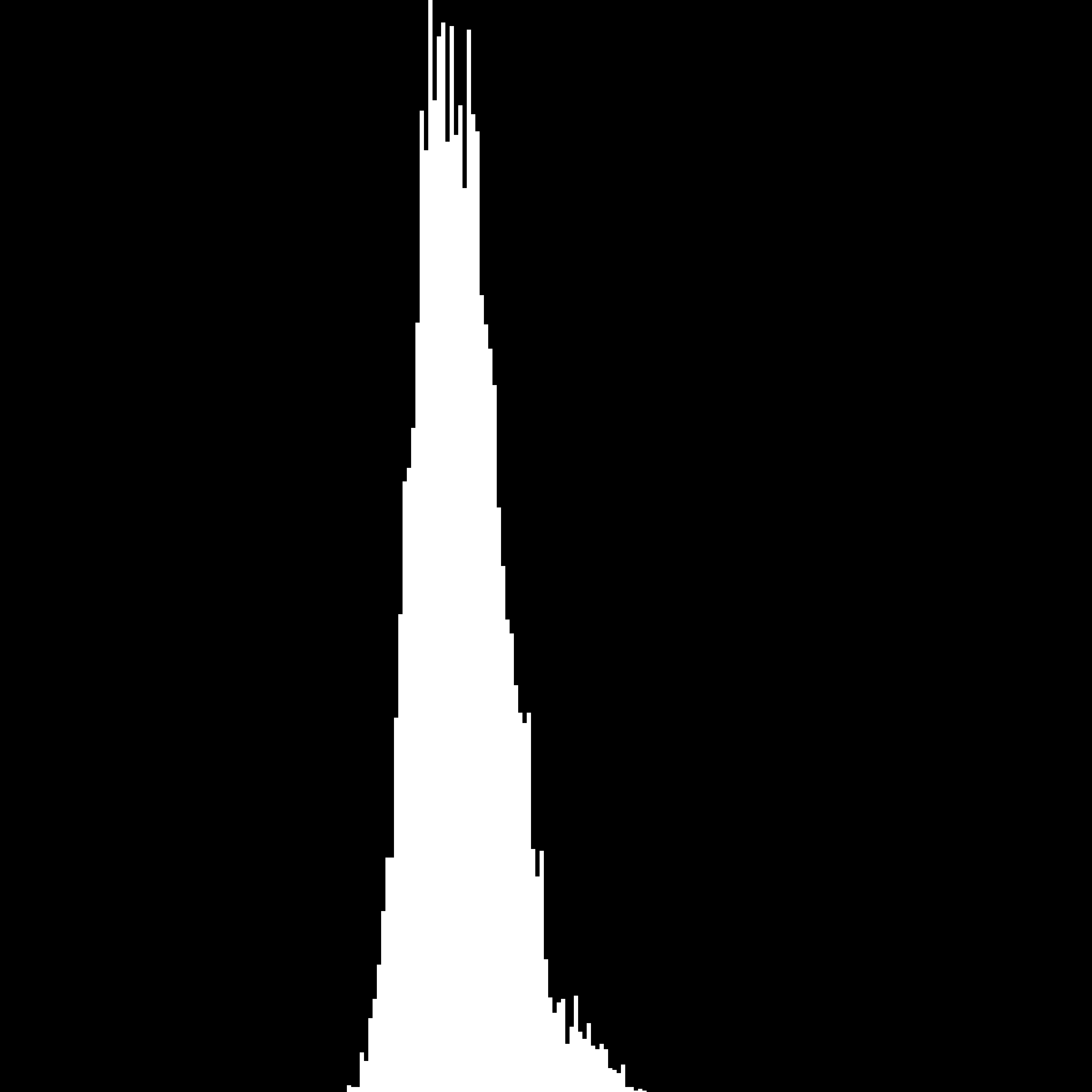
Для «плохих» участков яблока (у = 1):

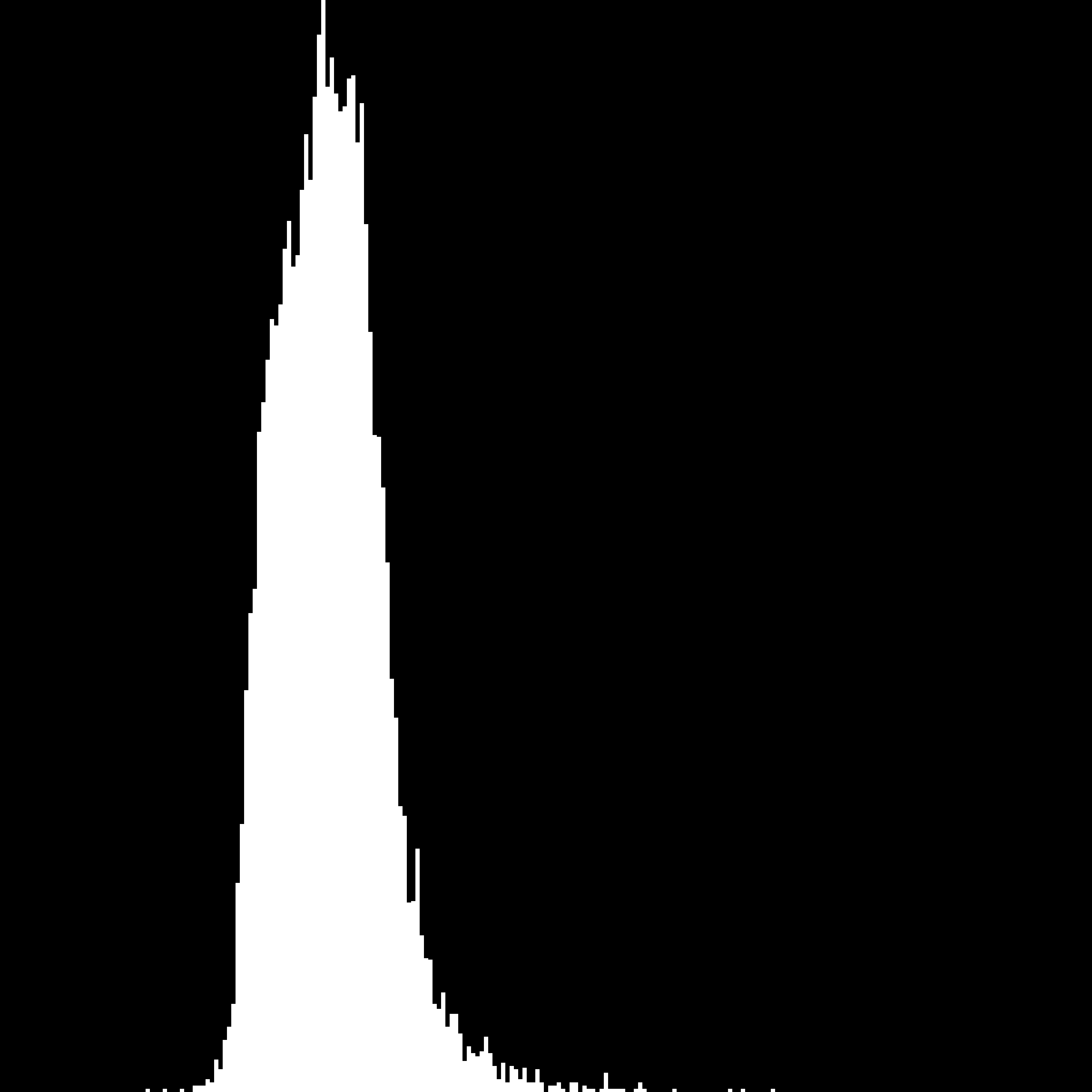
Я не уверен на 100%, что использование одних интенсивов даст желаемые результаты, но даже при этом использование его на четко отделимом наборе данных также не работает. Чтобы проверить это, я передал это, маркированное, полностью белое и полностью черное изображение. Затем я запускаю его на маленьком изображении ниже:

Даже на этом изображении не удается определить любой сегменты как черные.

Используя MSE, я вижу, что стоимость приближается к точке, где она остается, для черно-белого теста она начинается примерно с 250 и заканчивается на 100. Куски яблок начинаются примерно с 4000 и заканчиваются в 1600.

Что я не могу сказать, так это где проблемы.

Является ли подход обоснованным, но реализация нарушена? Является ли логистическая регрессия неправильным алгоритмом для этой задачи? Достаточно ли надежен градиент?