(линейный или многочленный) алгоритм регрессии для нижней границы почти синусоидальных данных
Мне нужно найти кривую, которая бы соответствовала нижним точкам моих дискретных данных. Линейная регрессия была бы в порядке, но многочленная была бы отличной 🙂
Обычно я не занимаюсь такой задачей, поэтому, пожалуйста, не обращайте на меня внимание, если это слишком простой вопрос. Я все еще занимаюсь исследованиями, но я подумал, что не мешало бы также спросить здесь.
Самое главное, что ни одна из точек не должна находиться под этой линией. Насколько я выяснил, обычная регрессия оценивает какую-то строку в середине данных, и это не очень хорошо для меня.
Какой алгоритм я могу использовать? Я собираюсь написать код на C ++, но пример на любом языке был бы великолепен.
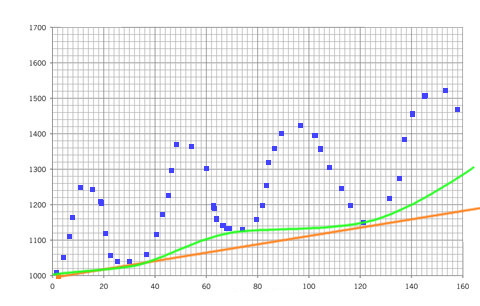
Графическое объяснение:
Синий — мои данные
Апельсин — достаточно хорошее решение
Зеленый — отличное решение!
Спасибо!
Решение
Ну, вы еще не предоставили нам соответствующие данные, поэтому я использовал ваше изображение в качестве входных данных. Линейная нижняя граница вычисляется довольно просто:
- вычислить ограничивающую рамку для ваших данных
- bin ищет «все допустимые» строки в bbox как нижнюю границу
Вот простой пример C ++:
//---------------------------------------------------------------------------
double *pnt=NULL; int pnts=0; // input data points pnt[pnts]={ x0,y0,x1,y1,x2,y2,... } loaded during init of app from image
double fit0[4]={0,0,0,0}; // output line endpoints fit0 = { x0,y0,x1,y1 }
//---------------------------------------------------------------------------
void compute()
{
int i,j;
double x,x0,x1,y,y0,y1,yy,a,a0,a1,X0;
// bbox
x0=x1=pnt[0]; X0=x0;
y0=y1=pnt[1];
for (i=0;i<pnts;)
{
x=pnt[i]; i++;
y=pnt[i]; i++;
if (x0>x) x0=x;
if (y0>y){y0=y; X0=x; } // X0 is the point where y is minimal
if (x1<x) x1=x;
if (y1<y) y1=y;
}
// fit0 (line)
fit0[0]=X0;
fit0[1]=y0;
fit0[2]=x1;
fit0[3]=y0;
for (a0=y0,a1=y1,j=0;j<10;j++) // bin search accuracy iterations
{
a=0.5*(a0+a1);
for (i=0;i<pnts;)
{
x=pnt[i]; i++; // tested point from data
y=pnt[i]; i++;
yy=y0+((x-X0)*(a-y0)/(x1-X0)); // coresponding y value of fited line
if (yy>y) { i=-1; break; } // too big
}
if (i>=0){ a0=a; fit0[3]=a; } // valid line
else a1=a; // invalid line
}
}
//---------------------------------------------------------------------------
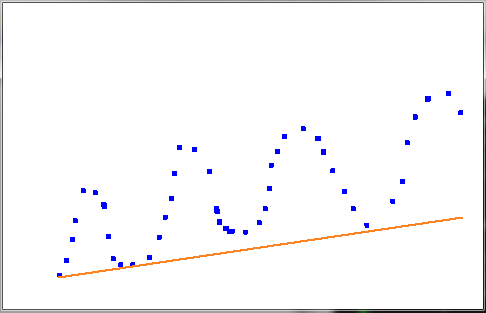
Поэтому я установил границу как линию. Его первой конечной точкой является первый глобальный минимум слева, и я бинарный поиск второй конечной точки. Где его x это глобальный максимум x а также y проверяется между глобальным минимумом и максимумом (лучшее решение запоминается). Вот предварительный просмотр:
Другие решения
Других решений пока нет …