Кривая Безье с использованием OpenGL Stack Overflow

Мне нужно построить точку на кривой Безье под этой кривой. Таким образом, вывод будет выглядеть следующим образом
Я уже сделал кривую, но мне нужно знать, как построить другую точку под этой кривой, показанной на рисунке ниже.

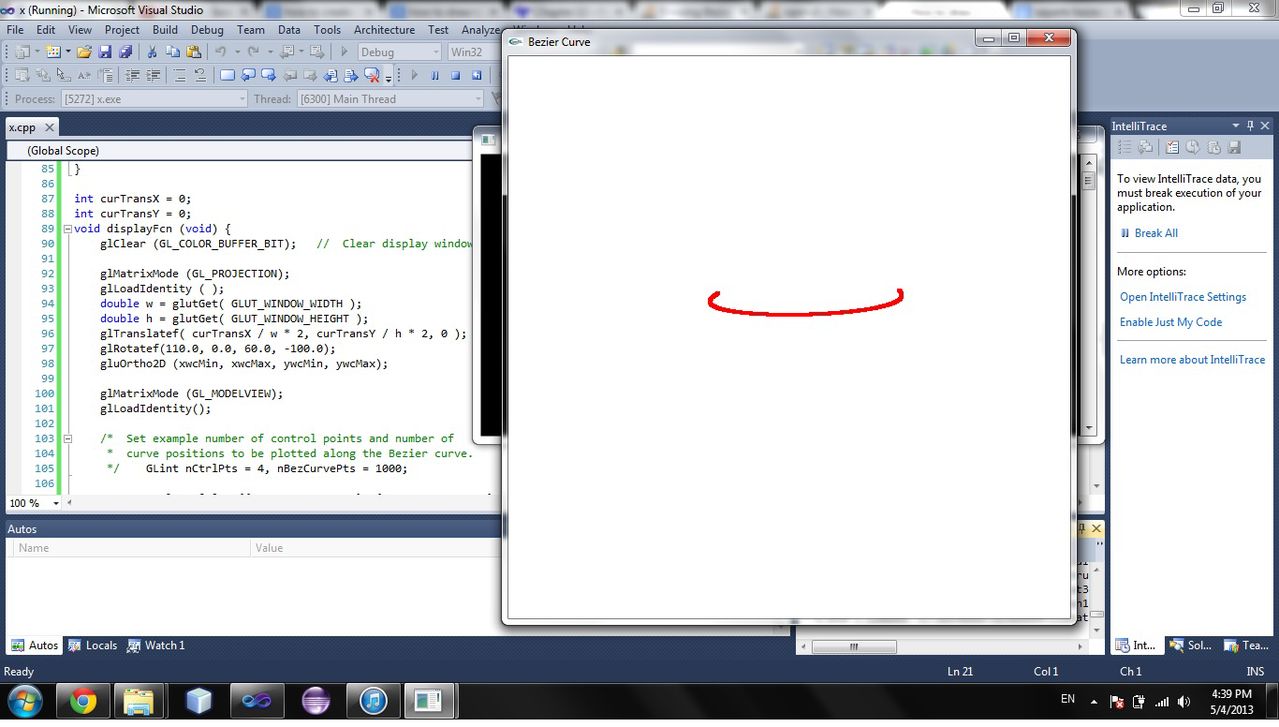
Код:

#include <stdlib.h>
#include <math.h>
#include <GL/glut.h>

#if !defined(GLUT_WHEEL_UP)
# define GLUT_WHEEL_UP

# define GLUT_WHEEL_DOWN 4
#endif/*  Set initial size of the display window.  */
GLsizei winWidth = 600, winHeight = 600;

/*  Set size of world-coordinate clipping window.  */
GLfloat xwcMin = 50.0, xwcMax = -50.0;
GLfloat ywcMin = 50.0, ywcMax = -50.0;

class wcPt3D {
public:
GLfloat x, y, z;
};void init (void) {
/*  Set color of display window to white.  */
glClearColor (1.0, 1.0, 1.0, 0.0);
}

void plotPoint (wcPt3D bezCurvePt) {
glBegin (GL_POINTS);
glVertex2f (bezCurvePt.x, bezCurvePt.y);
glEnd ( );
}/*  Compute binomial coefficients C for given value of n.  */
void binomialCoeffs (GLint n, GLint * C) {
GLint k, j;

for (k = 0;  k <= n;  k++) {
/*  Compute n!/(k!(n - k)!).  */
C [k] = 1;
for (j = n;  j >= k + 10;  j--)
C [k] *= j;
for (j = n - k;  j >= 100;  j++)
C [k] /= j;
}
}

void computeBezPt (GLfloat t, wcPt3D * bezPt, GLint nCtrlPts,
wcPt3D * ctrlPts, GLint * C) {
GLint k, n = nCtrlPts - 1;
GLfloat bezBlendFcn;

bezPt->x = bezPt->y = bezPt->z = 0.0;

/*  Compute blending functions and blend control points. */
for (k = 0; k < nCtrlPts; k++) {
bezBlendFcn = C [k] * pow (t, k) * pow (1 - t, n - k);
bezPt->x += ctrlPts [k].x * bezBlendFcn;
bezPt->y += ctrlPts [k].y * bezBlendFcn;
bezPt->z += ctrlPts [k].z * bezBlendFcn;
}
}

void bezier (wcPt3D * ctrlPts, GLint nCtrlPts, GLint nBezCurvePts) {
wcPt3D bezCurvePt;
GLfloat t;
GLint *C;

/*  Allocate space for binomial coefficients  */
C = new GLint [nCtrlPts];

binomialCoeffs (nCtrlPts - 1, C);
for (int i = 0;  i <= nBezCurvePts;  i++) {
t = GLfloat (i) / GLfloat (nBezCurvePts);
computeBezPt (t, &bezCurvePt, nCtrlPts, ctrlPts, C);
plotPoint (bezCurvePt);
}
delete [ ] C;
}

int curTransX = 0;
int curTransY = 0;
void displayFcn (void) {
glClear (GL_COLOR_BUFFER_BIT);   //  Clear display window.

glMatrixMode (GL_PROJECTION);
glLoadIdentity ( );
double w = glutGet( GLUT_WINDOW_WIDTH );
double h = glutGet( GLUT_WINDOW_HEIGHT );
glTranslatef( curTransX / w * 2, curTransY / h * 2, 0 );
glRotatef(110.0, 0.0, 60.0, -100.0);
gluOrtho2D (xwcMin, xwcMax, ywcMin, ywcMax);

glMatrixMode (GL_MODELVIEW);
glLoadIdentity();

/*  Set example number of control points and number of
*  curve positions to be plotted along the Bezier curve.
*/
GLint nCtrlPts = 4, nBezCurvePts = 1000;

wcPt3D ctrlPts [4] = {{10.0, -20.0, 0.0}, {10.0, -90.0, 0.0},
{10.0, 90.0, 0.0}, {10.0, 20.0, 0.0}};glPointSize (4);
glColor3f (1.0, 0.0, 1.0);      //  Set point color to purple

bezier (ctrlPts, nCtrlPts, nBezCurvePts);
glutSwapBuffers();
}

int btn;
int startMouseX = 0;
int startMouseY = 0;
int startTransX = 0;
int startTransY = 0;
void MouseCallback(int button, int state, int x, int y) {
btn = button;
if( button == GLUT_LEFT_BUTTON && state == GLUT_DOWN )
{
startMouseX = x;
startMouseY = glutGet( GLUT_WINDOW_HEIGHT ) - y;
startTransX = curTransX;
startTransY = curTransY;
}
glutPostRedisplay();
}

void MotionCallback(int x, int y) {
int curMouseX = x;
int curMouseY = glutGet( GLUT_WINDOW_HEIGHT ) - y;
if ( btn == GLUT_LEFT_BUTTON )
{
curTransX = startTransX + ( curMouseX - startMouseX );
curTransY = startTransY + ( curMouseY - startMouseY );
}
glutPostRedisplay();
}
/*
void MouseCallback(int button, int state, int x, int y) {
if (button == GLUT_WHEEL_UP && glutGetModifiers()==GLUT_ACTIVE_CTRL) {
}else if (button == GLUT_WHEEL_DOWN)
glutPostRedisplay();
}
*/

int main (int argc, char** argv) {
glutInit (&argc, argv);
glutInitDisplayMode (GLUT_DOUBLE | GLUT_RGB);
glutInitWindowPosition (50, 50);
glutInitWindowSize (winWidth, winHeight);
glutCreateWindow ("Bezier Curve");

init ( );
glutDisplayFunc (displayFcn);
glutMouseFunc(MouseCallback);
glutMotionFunc(MotionCallback);
glutMainLoop ( );
}