Корень квадратный из числа … Точность до п точности

Question

Корень квадратный из числа … Точность до п точности

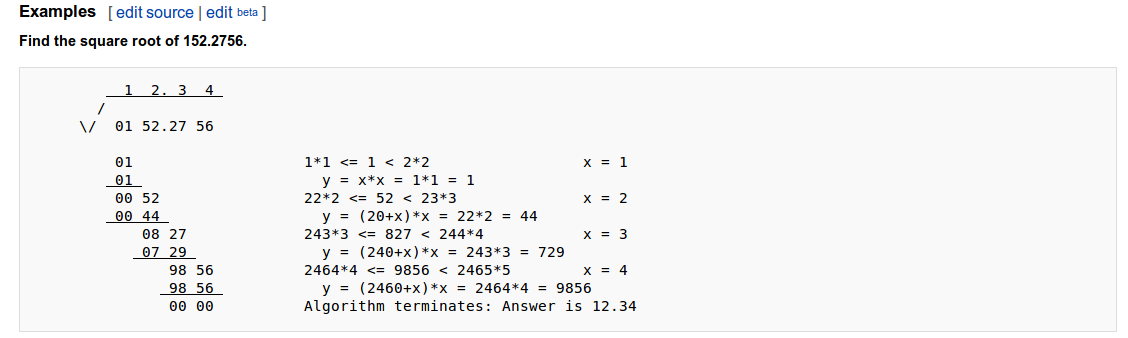
Метод, найденный в Википедии

Я не мог понять вышеуказанный метод. Может кто-нибудь объяснить, пожалуйста? Я сделал некоторый код, но он ограничен какой-то жестко закодированной точностью и, похоже, потребляет слишком много ресурсов компьютера.

R = 0.00001
INPUT N
WHILE R*R != N
R = R + 0.00001
ENDWHILE
PRINT R

Что такое код алгоритма или C ++ для квадратного корня числа с точностью до n?
N может быть взято от пользователя, если требуется.

-3

algorithm c++numerical-methods

Решение

Другие решения

Вот фрагмент кода C ++, хотя он не является произвольной точностью, он может быть вам полезен. Это немного ближе к полному решению, чем ваш основной код:

#include <iostream>
#include <vector>
#include <cstdlib>
#include <cstring>
#include <climits>

const unsigned g_unPlaces = 8;

int main(int argc, char** argv)
{
if (argc != 2)
{
std::cerr << "USAGE: " << *argv << " NUMBER" << std::endl;
return 1;
}

std::vector<unsigned> vecInteger;
std::vector<unsigned> vecDecimal;
char *pDecimal = strchr(argv[1], '.');

// Read integer part of NUMBER
if (pDecimal == NULL) pDecimal = argv[1] + strlen(argv[1]);
if ((pDecimal - argv[1]) % 2) vecInteger.push_back(0);
for (char *pCurrent = argv[1]; pCurrent < pDecimal; ++pCurrent)
{
int nValue = *pCurrent - '0';
if (nValue >= 10 || nValue < 0)
{
std::cerr << "Error: Invalid character in input!" << std::endl;
return 1;
}
vecInteger.push_back((unsigned) nValue);
}

// Read decimal part of NUMBER
if (*pDecimal != '\0')
{
for (++pDecimal; *pDecimal != '\0'; ++pDecimal)
{
if (*pDecimal == '.')
{
std::cerr << "Error: Multiple decimals in input!" << std::endl;
return 1;
}

int nValue = *pDecimal - '0';
if (nValue >= 10 || nValue < 0)
{
std::cerr << "Error: Invalid character in input!" << std::endl;
return 1;
}
vecDecimal.push_back((unsigned) nValue);
}
if (vecDecimal.size() % 2) vecDecimal.push_back(0);
}

const unsigned unInteger = vecInteger.size();
const unsigned unDecimal = vecDecimal.size();

std::vector<unsigned> vecValues;

unsigned x, y = 0, c = 0, p = 0;
for (unsigned i = 0; i < g_unPlaces; ++i)
{
if (2*i < unInteger-1)
{
c = (c*100 - y*100) + vecInteger[i*2]*10 + vecInteger[i*2+1];
}
else if (2*i < unInteger+unDecimal-1)
{
c = (c*100 - y*100) + vecDecimal[i*2-unInteger]*10
+ vecDecimal[i*2+1-unInteger];
}
else
{
c = c*100 - y*100;
}

if (c == 0) break;

y = 0;
for (x = 1; x < 10; ++x)
{
unsigned temp = x*(20*p + x);
if (temp > c) { --x; break; }
y = temp;
}

p = 10*p + x;
vecValues.push_back(x);
}

// Write the result
for (unsigned i = 0; i < unInteger/2; ++i)
{
std::cout << vecValues[i];
}
std::cout << '.';
for (unsigned i = unInteger/2; i < vecValues.size(); ++i)
{
std::cout << vecValues[i];
}
std::cout << std::endl;

return 0;
}

Что касается помощи в понимании вашего алгоритма, лучший подход — начать с самого начала и проработать каждый шаг. Попробуйте с небольшими значениями, такими как 4, 16 и 64. Пройдите пошаговый алгоритм с листком бумаги и карандашом и запишите части для каждого шага.

Если ваша цель состоит только в том, чтобы рассчитать число с точностью до N, то вам, вероятно, будет лучше использовать уже принятое решение, изменить свою проблему, чтобы вам не требовалась точность N, или взглянуть на некоторые другие комментарии / ответы.

0

Источник

Accepted Answer

Есть алгоритмы, которые намного лучше подходят для компьютерной оценки. Я изучил этот вопрос в 1960-х годах как способ ручного вычисления квадратного корня цифра за цифрой, используя процесс, похожий на длинное деление.

Цель при вычислении n-й цифры результата состоит в том, чтобы найти наибольшую строку префикса так, чтобы квадрат был меньше или равен первым 2n цифрам ввода.

Основная идея заключается в том, что (a+b)^2 = a^2 + b^2 + 2ab, В алгоритме a частичный результат до сих пор, и b это новая цифра. Он учитывает факторы 100 в квадрате и 10 в корне, перемещая два места на входе для одной сгенерированной цифры в результате.

Позволять p быть частичным результатом до добавления цифры d, Мы уже вычли p^2 от входа. Нам нужно также вычесть d^2 + 2pd, чтобы сохранить вычитание квадрата нового частичного результата. Эквивалентно, вычесть d(2p+d), Мы продолжаем p уже в два раза, добавить dи умножить на d, Прежде чем перейти к следующему шагу, нам нужно удвоить d также.

0