Код линейной интерполяции в Википедии — я не понимаю

Question

Код линейной интерполяции в Википедии — я не понимаю

Я читаю следующий код (взят из Вот)

void linear_interpolation_CPU(float2* result, float2* data,
float* x_out, int M, int N) {
float a;
for(int j = 0; j < N; j++) {
int k = floorf(x_out[j]);
a = x_out[j] - floorf(x_out[j]);
result[j].x = a*data[k+1].x + (-data[k].x*a + data[k].x);
result[j].y = a*data[k+1].y + (-data[k].y*a + data[k].y);
}
}

но я не понимаю

Почему результат [y] не рассчитывается с помощью

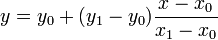
введите описание изображения здесь

формула?

7

c++interpolation

Решение

Другие решения

Других решений пока нет …

Источник

Accepted Answer

Это рассчитывается таким образом.

Посмотрите на первые две строки:

int k = floorf(x_out[j]);
a = x_out[j] - floorf(x_out[j]);

Первая строка определяет x0 используя функцию пола. Это связано с тем, что в статье предполагается, что интервал решетки равен единице для точек выборки в соответствии с линией:

the samples are obtained on the 0,1,...,M lattice

Теперь мы могли бы переписать вторую строку для ясности как:

a = x_out[j] - k;

Поэтому вторая строка x-x0,

Теперь давайте рассмотрим уравнение:

result[j].y = a*data[k+1].y + (-data[k].y*a + data[k].y);

Переписать это с точки зрения y, x, а также x0 дает:

y = (x-x0)*data[k+1].y + (-data[k].y*(x-x0) + data[k].y);

Давай переименуем data[k+1].y как y1 а также data[k].y как у0:

y = (x-x0)*y1 + (-y0*(x-x0) + y0);

Давайте изменим это, вытаскивая x-x0:

y = (x-x0)*(y1-y0) + y0;

И переставить еще раз:

y = y0 + (y1-y0)*(x-x0);

Опять же, шаг решетки важен:

the samples are obtained on the 0,1,...,M lattice

Таким образом, x1-x0 всегда 1. Если мы вернем его обратно, мы получим

y = y0 + (y1-y0)*(x-x0)/(x1-x0);

Какое уравнение вы искали.

Конечно, смешно, что код написан не для того, чтобы сделать это очевидным.

12