Код C / C ++ с научной библиотекой GNU (GSL) дает разные результаты для GNUPlot — возможная нестабильность с плавающей запятой?
GNUPlot гораздо лучше подходит для моих данных, чем мой код GSL. Зачем?
Я немного запутался в данный момент, поэтому мой вопрос может быть не очень хорошо сформулирован … Я буду редактировать его по мере улучшения моего понимания.
Оригинальный заголовок этого вопроса был: «g ++ Компиляция кода с флагами -o1 -o2 или -o3 и точностью с плавающей запятой»
Я считаю, что мой код страдает от числовой нестабильности.
GNUPlot обеспечивает гораздо лучшее соответствие моим данным, чем мой код GSL, что удивительно, поскольку я считаю, что GNUPlot также использует библиотеки GSL?
Я написал код на C / C ++, в котором используется научная библиотека GNU (GSL). Мой код соответствует нелинейным функциям для наборов нелинейных данных. Алгоритмы, которые делают это, могут быть очень чувствительны к порядку, в котором выполняются операции с плавающей запятой, из-за природы числовых неточностей, которые приводят к накоплению числовых ошибок округления.
Вопрос: «Может ли это быть вызвано эффектом запуска с одним из флагов оптимизации, -o1, -o2 или же -o3?»
Частичный ответ: я отключил любой -oN отметив и перекомпилировав мой код, я могу изменить результаты на небольшое количество, то есть: delta_x / x ~= 1.0e-3, Подгонка по-прежнему оставляет желать лучшего по сравнению с GNUPlot.
Функции, которые мне подходят:
Я предоставил их, чтобы показать вам численную работу, которая происходит. Я подозреваю, что некоторые из них склонны к числовым ошибкам.
Типичные значения для Yi будет в диапазоне 0.0 в 1.0, t как правило, в диапазоне 0.0 в 200.0, (Но подгонка плохая в первой половине этого диапазона.)
// Block A - Weighted Residuals
double t = time; // whatever that may be
double s = sigma[ix]; // these are the errors, tried 1.0 and 0.001 with no affect on parameter values obtained
double Yi = (std::sqrt(rho) * r0) / std::sqrt((rho - r0*r0) * std::exp(-2.0 * t / tau) + r0*r0); // y value - model
gsl_vector_set(f, ix, (Yi - y[ix])/sigma[ix]); // weighted residual
// Block B - Jacobian
double MEM_A = std::exp(-2.0 * t / tau); // Tried to do some optimization here
double MEM_B = 1.0 - MEM_A; // Perhaps this is causing a problem?
double MEM_C = rho - r0 * r0;
double MEM_D = MEM_C * MEM_A + r0*r0;
double MEM_E = std::pow(MEM_D, 1.5);
double df_drho = (std::pow(r0, 3.0) * MEM_B) / (2.0 * std::sqrt(rho) * MEM_E);
double df_dr0 = (std::pow(rho, 1.5) * MEM_A) / MEM_E;
double df_dtau = -1.0 * (std::sqrt(rho) * r0 * MEM_C * MEM_A * t) / (tau * tau * MEM_E);
gsl_matrix_set(J, ix, 0, df_drho / s);
gsl_matrix_set(J, ix, 1, df_dr0 / s);
gsl_matrix_set(J, ix, 2, df_dtau / s);
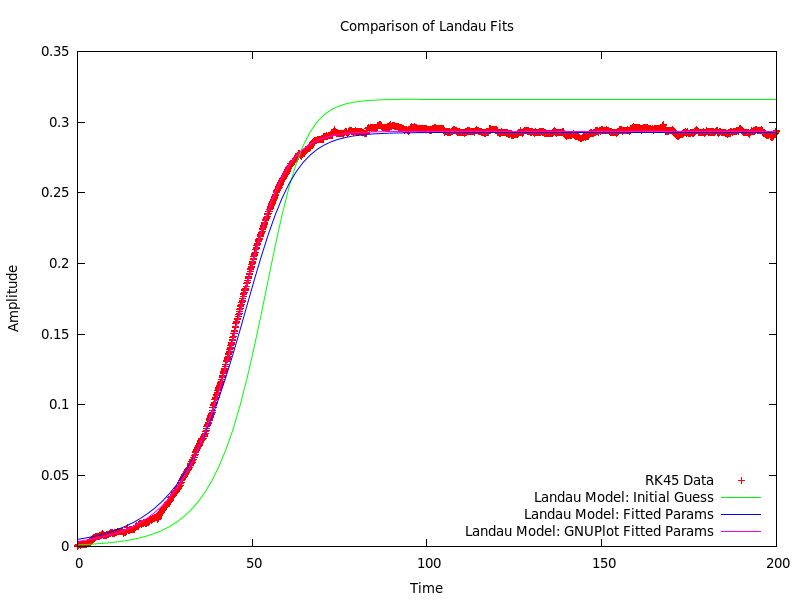
Ну вот график, который объясняет проблему намного лучше, чем я смог на словах. Вы можете игнорировать зеленую линию, это просто показывает начальные параметры, заданные до запуска алгоритма подгонки, который изменяет эти параметры.
Результаты GNUPlot Fit:
RHOFIT = 0.086173236829715 +- 2.61304934752193e-05
R0FIT = 0.00395856812689133 +- 2.08898744280108e-05
TAUFIT = 11.7694359189233 +- 0.016094629240588
// Not sure how GNUPlot calculates errors - they do not appear to be the regular errors computed from the off diagonal elements of the LM matrix after fitting. (If you know a little about the Levenberg–Marquardt algorithm.)
C ++ GSL Fit Результаты:
rho = 0.08551510 +/- ...
r0 = 0.00507645 +/- ... // Nonsense errors due to "not-real" errors on data points
tau = 12.99114719 +/- ...
При тщательном осмотре вы увидите, что линии Pink и Blue не накладываются друг на друга с довольно значительным запасом. Линия Pink — это то, что многие называют «хорошей подгонкой». Синяя линия для сравнения не особенно хороша.
Я попытался сделать панели ошибок (хотя они имеют одинаковый размер для всех точек — они не являются «реальными» панелями ошибок, только искусственными) меньше — это не помогает, только изменяет значение хи-квадрат и связанные ошибки каждого параметр после примерки.
- Я неправильно построил GSL?
- Gnuplot разбивает набор данных на маленькие блоки, чтобы числа были сложены примерно одинакового порядка? (Вроде как работает БПФ.)
iter: 0 x = 0.1 0.001 10 |f(x)| = 12487.8
status = success
iter: 1 x = 0.0854247 0.00323946 13.2064 |f(x)| = 10476.9
dx vector: -0.0145753, 0.00223946, 3.20642
status = success
iter: 2 x = 0.0854309 0.00576809 13.7443 |f(x)| = 3670.4
dx vector: 6.18836e-06, 0.00252863, 0.537829
chisq/dof = 6746.03
rho = 0.08543089 +/- 0.00013518
r0 = 0.00576809 +/- 0.00013165
tau = 13.74425294 +/- 0.09012196
Решение
Я наткнулся на эту страницу, потому что у меня была точно такая же проблема. Мне нужно было согласовать функцию с GSL, раньше я этого не делал, поэтому я сравнивал результаты с процедурой подгонки gnuplot. В моем случае я подгонял простой степенной закон к части энергетического спектра галактики, и GSL давал мне припадки, которые имели chi ^ 2 / DoF около 6.
Чтобы решить это, я понял, что был небрежным и Икс значения для моих точек данных не соответствуют Икс значения, в которых оценивалась функция подбора. Самый простой способ исправить это — создать сплайн из значений данных, а затем оценить сплайн на том же уровне. Икс значения, в которых будет оцениваться функция подбора. Например:
#include <gsl/gsl_spline.h>
.
.
.
std::vector< double > xvals;
std::vector< double > yvals;
fin.open("SomeDataFile.dat", std::ios::in);
while (!fin.eof()) {
double x, y;
fin >> x >> y;
xvals.push_back(x);
yvals.push_back(y);
}
fin.close();
gsl_spline *Y = gsl_spline_alloc(gsl_interp_cspline, yvals.size());
gsl_interp_accel *acc = gsl_interp_accel_alloc();
gsl_spline_init(Y, &xvals[0], &yvals[0], yvals.size());
double y[N];
for (int i = 0; i < N; ++i) {
double x = xmin + i*dx; // Where xmin is the smallest x value and dx
// is (xmax-xmin)/N
y[i] = gsl_spline_eval(Y, x, acc);
}
Затем в моей функции, где вычислялась разница между степенным законом и данными, я использовал те же xmin и dx, чтобы Икс значения были одинаковыми для функции Yi в вашей записи.
struct data {
size_t n;
double *y;
double xmin;
double xmax;
};
int powerLaw(const gsl_vector *x, void *dat, gsl_vector *f) {
size_t n = ((data *) dat)->n;
double *y = ((data *) dat)->y;
double xmin = ((data *) dat)->xmin;
double xmax = ((data *) dat)->xmax;
double dx = (xmax-xmin)/double(n);
double A = gsl_vector_get(x, 0);
double alpha = gsl_vector_get(x, 1);
for (int i = 0; i < n; ++i) {
double xval = xmin + double(i)*dx;
double Yi = A*pow(xval,alpha);
gsl_vector_set(f, i, Yi - y[i]);
}
return GSL_SUCCESS;
}
После этого значения из gnuplot и GSL довольно хорошо согласуются, gnuplot дает амплитуду 123.196 +/- 0,04484, а показатель степени -1.13275 +/- 0.001903, а GSL дает 123.20464 +/- 0.98008 и -1.13272 +/- 0.00707. Результаты подгонки показаны на графике ниже, где Fit от gnuplot, а g (x) от GSL (Примечание: я не ожидаю, что степенные законы будут точно соответствовать данным, но достаточны для мои цели). Посадки у gnuplot и GSL практически идентичны.
График данных и подходит от gnuplot и GSL.
Я бы просто упомянул об этом в комментарии к вашему вопросу, но так как мне никогда не приходилось задавать вопрос здесь и никогда не отвечал на него, мне не хватило представителя.
Другие решения
