KNN поиск с подписанными метриками
Я ищу библиотеку C ++, которая позволяет эффективно находить k-ближайших соседей точки в наборе точек, используя квадратную псевдорму:
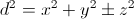
где моя третья координата может иметь или не иметь знак минус в своей квадратной норме. В качестве альтернативы я могу рассмотреть четырехмерное пространство, где третий компонент всегда имеет положительный знак, а четвертый всегда отрицательный знак.
В документации библиотеки ANN говорится, что она может использовать любую метрику «Минковского». Показанная выше метрика является определением метрики Минковского (в смысле Wolfram Mathworld , но не в смысле ANN). Тем не менее, ANN кажется гибким и требует только операторов «+» и «-» (ANN документация, страница 14), но они определены не для каждого компонента, а для всего мира.
Кто-нибудь когда-либо обобщал ANN, чтобы обращаться с таким случаем? Это тривиально? Разве это не испортит kd-дерево? Существует ли другая библиотека для этого?
Спасибо!
Решение
Норма х2+Y2-Z2 нарушает некоторые допущения, на которых обычно используется поиск с использованием kd-дерева. Одно из этих предположений состоит в том, что «соседство» («близость») является некоторым «локальным» свойством, то есть с учетом точки P все точки Q с dist(P,Q) < r иметь координаты в конечном диапазоне вокруг координат P. Таким образом, разделение точек, установленных вдоль их координат, может быть использовано для эффективного поиска. Но по вышеуказанной норме даже для точек Q с dist([0,0,0],Q) = 0 конечная коробка не может быть дана; точки лежат на бесконечном конусе. Тем не менее, должна быть возможность разработать эффективный алгоритм поиска, который использует «конусную» структуру, но kd-дерево не будет работать.
Другие решения
Других решений пока нет …
