Какой алгоритм я должен использовать, чтобы найти минимальный поток на орграфе, где существуют нижние, но не верхние границы потока?

Question

Какой алгоритм я должен использовать, чтобы найти минимальный поток на орграфе, где существуют нижние, но не верхние границы потока?

Какой алгоритм я должен использовать, чтобы найти минимальный поток на орграфе, где есть нижние границы, но не верхние границы потока? Например, этот простой пример:

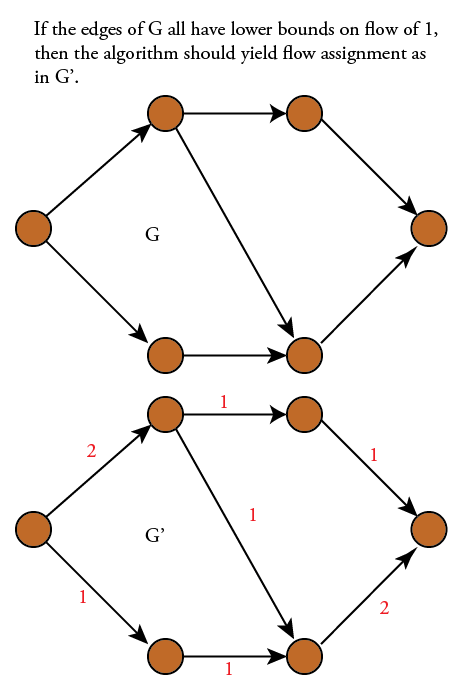
Схема простого примера. Источник: & lt; jwezorek.com/wp-content/uploads/2013/09/min_flow.png>

В литературе это проблема минимальных затрат. Однако в моем случае стоимость такая же, как и ненулевая нижняя граница потока, необходимого для каждого ребра, поэтому я сформулировал вопрос, как указано выше. В литературе вопрос будет таким: каков наилучший алгоритм для нахождения минимального потока затрат для ориентированного ациклического графа с одним источником / одним стоком, в котором каждое ребро имеет бесконечную емкость, ненулевую нижнюю границу потока и стоимость равна нижней границе потока.

Из моего исследования кажется, что основной способ, которым люди справляются с любой минимальной стоимостью любой сети, состоит в том, чтобы поставить проблему как Проблема типа LP и решить таким образом. Моя интуиция, однако, заключается в том, что нет верхних границ потока, т.е. Наличие ребер с бесконечными емкостями облегчает проблему, поэтому мне было интересно, есть ли алгоритм, специально предназначенный для этого случая, использующий больше «графических» техник, чем симплекс-метод et. и др.

Я имею в виду, если все затраты и нижние границы равны 1, как указано выше … тогда мы ищем поток, который покрывает все ребра, подчиняется правилам потока и не продвигает слишком большой поток через любой путь от s до t , Мне просто кажется, что для этого не нужно требовать решения для LP, и действительно, статья в Википедии о минимальных потоках затрат гласит, что «если ограничение емкости устранено, проблема сводится к проблеме кратчайшего пути», но я думаю, что они говорят о случай, когда все нижние оценки равны нулю.

Также есть ли где-нибудь открытый код C / C ++ для минимального потока затрат? По поиску того, что доступно, я обнаружил, что я могу либо сам решить проблему как проблему LP и решить ее с помощью решателя LP с открытым исходным кодом, либо я мог бы использовать LEMON, который предоставляет несколько алгоритмов для минимизации затрат. Насколько я могу судить, библиотека графов наддува не включает реализацию.

Есть ли еще что-нибудь?

7

c++graph-algorithm linear-programming network-flow

Решение

Другие решения

Написание решателя нетривиально.

Смотрите библиотеку LEMON (часть COIN-OR). Он имеет ряд высоко оптимизированных алгоритмов для решения проблемы минимальных затрат. Вы можете выбрать, какой алгоритм лучше всего работает с вашими данными.

Увидеть http://lemon.cs.elte.hu/trac/lemon для получения информации о ЛИМОН.

Увидеть http://lemon.cs.elte.hu/pub/doc/1.3/a00607.html для получения подробной информации о минимальной стоимости сетевого потока.

3

Добавьте все «нижние границы» потоков на каждом ребре: в любом случае это будет необходимо для любого возможного решения.

Для каждого узла n в топологическом порядке (т.е. по краям) от раковины t, если сумма S- из того, что идет в краю, больше, чем сумма S+ из того, что выходит, затем добавить поток S+ - S- по всем краям кратчайшего пути между s а также t (составьте список кратчайшего пути, делая это для эффективности).

Затем у вас есть «минимальное» назначение (в том смысле, что оно необходимо в каждом возможном решении), такое как S+ - S- является неотрицательным в каждом узле, и минимальная емкость удовлетворяется на каждом ребре.

Затем проблема сводится к задаче с несколькими потоками на той же структуре графа:

источник тот же;
нет предела мощности;
каждый узел, где S+ - S- строго положительно становится раковиной с требуемым потоком S+ - S-,
начальная раковина (которая имела требуемый поток F) становится раковиной с потоком F - S- если F-S- неотрицательно (в противном случае начальное ограничение будет удовлетворено любым решением).

Изменить: для вашей проблемы график выглядит следующим образом

     x1 -- x2
/   \     \
s      \     t
\     \   /
x3 -- x4

с минимальной емкостью 1 для каждого ребра, и я предполагаю, что минимальный поток не требуется в приемнике t,

Сначала присвойте 1 каждому ребру.

Различия S+ - S- для каждого узла (кроме, конечно, s а также t) является:

x1: 1
x2: 0
x3: 0
x4: -1

единственный минус для x4; мы добавляем 1 к каждому краю на кратчайшем пути из x4 в tв таком случае к краю (x4, t),

Сейчас S+ - S- неотрицателен для каждого узла и положителен только для x1; проблема сводится к многопотоковой задаче (в этом случае это простая задача потока), где запрошенный поток 1 в x1и источник до сих пор s,

1

Источник

Accepted Answer

При отсутствии верхних границ самый простой способ — самый простой в реализации, понимании и достаточно эффективном — найти минимальный поток графа состоит в следующем:

Найдите допустимый поток, то есть поток, который удовлетворяет правилам потока и нижним пределам потока, но не обязательно является минимальным потоком. Это может быть достигнуто путем прохождения графа в глубину, отслеживания текущего пути во время прохождения и при посещении ранее обнаруженного узла или t, целевого узла, увеличения потока на текущем пути с максимальным меньшим привязка неудовлетворенных ребер на текущем пути вплоть до t.
Превратите допустимый поток в минимальный поток, решив проблему максимального потока. Вам нужно найти максимальный поток на графике, который имеет пропускную способность, равную потоку (e) — нижняя граница (e), где поток (e) означает поток из допустимого потока. Этот максимальный поток, вычтенный из возможного потока, будет минимальным потоком.

Версия выше также может быть выполнена в случае, когда график также имеет верхние границы потока. В этом случае шаг 1. является более сложным, но может быть решен путем выполнения начального вычисления максимального потока на специально построенном графике.

6