Какая математика стоит за такими анимационными траекториями?
Какая математика стоит за чем-то вроде этого? C ++ перспектива.
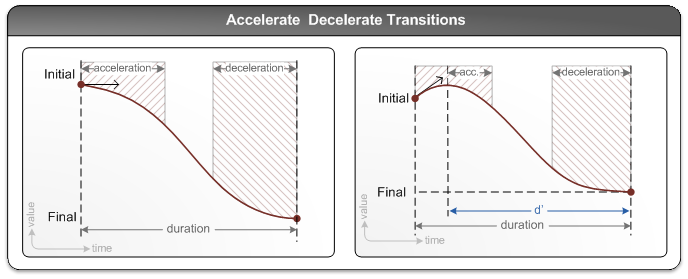
Больше примеров по этому Страница MSDN здесь.
ОБНОВИТЬ: Был задан более конкретный вопрос. Для чего нужна теория математики / анимации? Подростки Пеннера? Как вы пришли к этим формулам? На каких математических принципах они основаны?
Я и математика, мы не лучшие друзья! Я работаю надFLOAT Значение аниматора для пользовательского интерфейса я пишу, и мне было интересно, что математика с точки зрения нативного программиста C ++ для создания такой траектории.
Погуглил и нашел код, но я также ищу немного теории с точки зрения программирования… не просто код или чистая математика. Я могу собрать нужный мне код из того, что нашел в Интернете, но я бы хотел понять его в процессе. Как этот сайт, который позволяет экспериментировать с генератор функций ослабления.
Я также мог бы использовать Диспетчер анимации Windows (и я мог бы, если вещи становятся кровавыми), но это действует на одного float, И просто анимация RGB требует анимации каждого FLOAT отдельно. Это приводит к огромному взлому кода … очень плохо.
Если у кого-то есть намеки, я был бы очень признателен. Я ищу в основном теорию с точки зрения программирования. Конечная цель состоит в том, чтобы написать набор различных алгоритмов анимации, которые могут анимировать набор FLOAT от их начальных значений до их целевых значений за период времени или скорости и тому подобное.
План состоит не только в написании кода, но и в понимании того, что происходит за ним. А потом, возможно, проявите творческий подход с помощью этой анимации … если только они не окажутся жесткими стандартными математическими функциями.
Решение
Математика есть математика это математика
Хороший учебник по Риманова сумма продемонстрирует концепцию.
В фундаментальном программировании у вас есть математическое уравнение, которое генерирует значение Y (высоту) для данного X (времени). Периодически, например, раз в секунду, вы подключаете новое значение X (время) и возвращаете высоту.
Чем чаще вы оцениваете эту функцию, тем лучше разрешение (именно здесь приходят диаграммы суммы Римана и исчисления). Лучшее, что вы получите, это приближение к кривой, которая выглядит как ступеньки лестницы.
Во встроенных системах не так много ресурсов, чтобы очень часто оценивать такую функцию. Кривая может быть аппроксимирована с использованием отрезков. Чем больше отрезков, тем лучше аппроксимация (повышает точность). Таким образом, один метод состоит в том, чтобы разбить кривую на отрезки. Для заданного x используйте соответствующую линейную формулу для линии. Оценка линии обычно требует меньше ресурсов, чем оценка уравнения более высокой степени.
Ваши кривые обычно генерируются из уравнений физики. Так что вам нужно не только улучшать математику, но и физику.
В противном случае вы можете искать в Интернете библиотеки, которые обрабатывают траектории.
По мере приближения к аппаратному обеспечению таймер может использоваться для вызова метода, который оценивает функцию траектории для данного X. Таймер помогает получить более точное значение времени.
Поищите в Интернете «алгоритм подбора кривой», «алгоритм Брезенхэма», «алгоритмы обнаружения конфликтов графики»
Другие решения
Так что подумайте о требованиях к функции анимации.
- Функция должна представлять действительное плавное движение между двумя положениями / состояниями. Для тех, кто не читал соответствующий раздел книги, это означает, что
fдолжна быть непрерывной и дифференцируемой функцией, такой, чтобыf(0) == 0а такжеf(1) == 1; реальные движения строятся с использованием этого в качестве примитива. - «Легкость» (в смысле анимации анимации) означает «производная равна нулю»; это дает эффект того, что движение начинается и / или заканчивается с нулевой скоростью (то есть остановка). Так что «легкость» означает
f'(0) == 0и «ослабление» означаетf'(1) == 0,
Все остальное основано на эстетических соображениях.
Кубические кривые (например, сплайны Безье / Эрмита) популярны отчасти потому, что они позволяют вам контролировать положение и тангенс (скорость) на обоих концах кривой, а также потому, что они близки к естественной форме, которую принимает гибкий луч, если вы ограничиваете его положение это в нескольких точках. Кубическая форма минимизирует внутреннее напряжение изогнутой балки. (Неудивительно, что эти деревянные балки известны дизайнерам лодок и другим составителям как «сплайны», потому что именно здесь мы получаем слово.)
Исторически рисованные мультипликационные аниматоры всегда определяли своих подростков по ощущениям, основываясь на опыте. Ключевые аниматоры рисуют диаграмму (называемую «временной диаграммой»; посмотрите ее в вашей любимой поисковой системе изображений) на стороне своих ключевых рисунков, которые сообщают промежуточным звенам, как следует рассчитывать промежуточные кадры.
Движение камеры (панорамирование, масштабирование, вращение), однако, было другим вопросом. Художники по макету / анимации указали начало и конец движения (указано с помощью полевой диаграммы), количество кадров, в течение которых будет происходить движение, инструкции по смягчению и все остальное, что команда макета / анимации сочла важным (например, если у вас было задержаться»).
Фактические движения должны быть рассчитаны; аудитория заметила бы, если бы один кадр поворота отсутствовал даже на пару сотых градуса. Выполнение этих расчетов было частью работы операторского отдела.
Есть замечательная книга под названием «Базовые приемы анимации» Брайана Солта, которая датируется еще во времена физических анимационных камер, и в некоторых деталях описывается, что они должны были делать и в какой степени. Я рекомендую это, если вы вообще заинтересованы в этом материале.
