Как вычислить синус огромных чисел
В течение нескольких дней мне было интересно, как можно было бы вычислить синус огромных чисел с величиной вокруг 100000! (радиан). Факториал — это просто пример, само число может быть любым, а не просто факториальным продуктом …) Я, очевидно, не использую double но cpp_rational из библиотеки повышения точности. Но я не могу просто сделать 100000! mod 2pi а затем использовать встроенную функцию sinl (Мне не нужно больше 10 десятичных цифр ..), так как мне нужно несколько миллионов цифр числа пи, чтобы сделать это точно.
Есть ли способ добиться этого?
Решение
В общем, это нетривиальная задача, так как она имеет много общего с Проблема дискретного логарифма, что в свою очередь подразумевает вычислительно интенсивный расчет.
Тем не менее, ваш расчет может быть проще, если вы рассмотрите логарифм 100000!/pi, поскольку он сводится к сумме логарифмов всех натуральных чисел, равных или меньших, чем 100000и вычитание: log(N!/pi) = \sum_{i=0}^N (log i) - log(pi), Если вы возведете это число в ряд, у вас будет приблизительная оценка (N!/pi), Вычтите целую часть и умножьте результат на pi, Это оценка вашего N! mod pi,
В формуле:
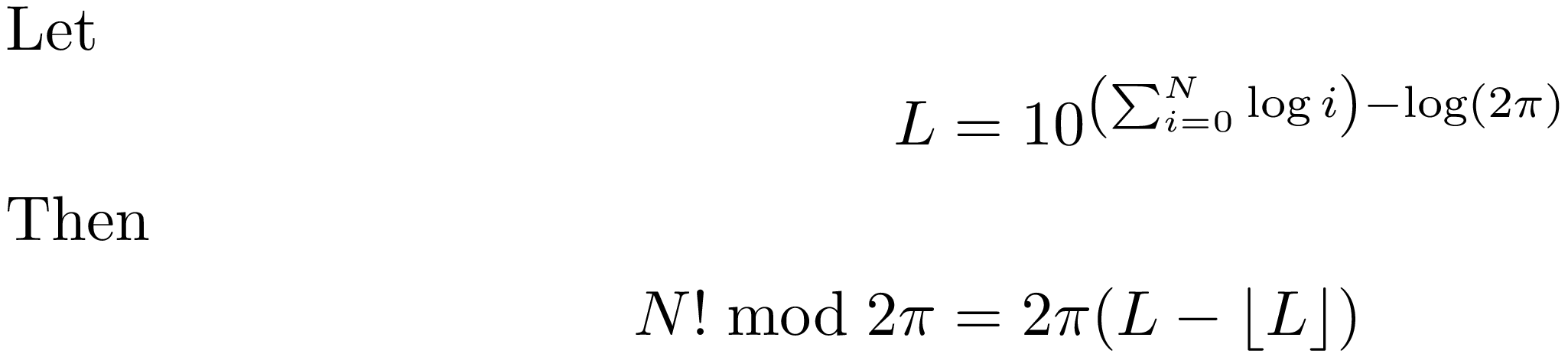
Как вы можете заметить, я много раз использовал слово приближенный. Это связано со следующими соображениями:
- Вы должны рассчитать много
logс, которые имеют некоторые затраты и ошибки - вы можете изменить основание вашего журнала в соответствии с размером вашей проблемы; это снова будет влиять на точность и точность вашего результата
- Вы должны возвести в степень обратно: маленькие ошибки могут привести к большим
- вычитать большие числа: может привести к большим отменам
- умножить на
piи оценитьsin: опять ошибки
Если вы считаете, что это может быть полезным, рассмотрите возможность использования Приближение Стирлинга.
В заключение отметим, что решение подобных проблем не является легким, вам всегда приходится иметь дело с ними в каждом конкретном случае.
Другие решения
Википедия перечисляет много тригонометрических тождеств. Некоторые включают продукты в аргумент, такие как Метод Чебышева который является рекурсивным, но рекурсия может быть уменьшена с помощью Полиномы Чебышева и / или запоминание. Если ваш аргумент так же легко факторизовать, как факториал, то это может быть осуществимым методом.
Примечание: = пи
Вычислить грех очень большого числа в радианах
(Измените их на кратные , разделив на 3.1415)
1. Обратите внимание: sin 0 = 0, sin 0.5pi = 1, sin pi = 1, sin1.5pi = -1, sin 2pi = 0
2. Четные или нечетные целочисленные значения перед пи, грех равен 0
3. Для действительных значений (с десятичными точками), для четных чисел перед десятичной запятой, возьмите его в качестве 0-го в качестве значения синуса, для нечетного, затем в качестве 1-го — в качестве значения синуса.
4. Смотрите примеры
* Обратите внимание, что грех и косинус имеют периодическую природу, поэтому это можно сделать таким образом для больших или малых чисел. 🙂
Например. (Используйте свои калькуляторы, чтобы проверить расчеты)
1,0 в радианах: грех 100 = -0,506
Разделите на 3.1415
Сделать в град
Sin 31.831pi (31.831 — действительное значение) = sin1.831 (180) = -0.506, проверка
2,0 в радианах: грех 50 = -0,2623
Разделите на 3.1415
Сделать в град
Sin 15,9155pi = sin1,9155 (180) = -0,2623
3,0 в радианах: грех 700 = 0,5439
Разделите на 3.1415
Сделать в град
Sin 222,8169pi = sin0,8169 (180) = -0,5440, проверка
4,0 в радианах: грех 15000 = 0,8934
Разделите на 3.1415
Сделать в град
Sin 4774,6483pi = sin0,6483 (180) = 0,893, проверка
Вы можете видеть, что все ответы проверены при непосредственном расчете значений с помощью калькулятора в радианном режиме. Надеюсь, это полезно.
Если вы хотите написать вычислительную программу, удачи в выяснении алгоритма.
Может быть, вы можете использовать cpp_rational для вычисления синуса непосредственно из вашего очень большого числа:
sin(x): x/1! - x^3/3! + x^5/5! - x^7/7! + ...
Повторяйте эту серию до тех пор, пока (для вашего приложения) не произойдут значительные изменения. Таким образом, вы полностью избегаете числа пи.
