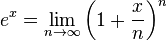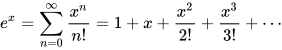Как вы обрабатываете exp () с SSE2?
Я делаю код, который по существу использует преимущества SSE2 для оптимизации этого кода:
double *pA = a;
double *pB = b[voiceIndex];
double *pC = c[voiceIndex];
for (int sampleIndex = 0; sampleIndex < blockSize; sampleIndex++) {
pC[sampleIndex] = exp((mMin + std::clamp(pA[sampleIndex] + pB[sampleIndex], 0.0, 1.0) * mRange) * ln2per12);
}
в этом:
double *pA = a;
double *pB = b[voiceIndex];
double *pC = c[voiceIndex];
// SSE2
__m128d bound_lower = _mm_set1_pd(0.0);
__m128d bound_upper = _mm_set1_pd(1.0);
__m128d rangeLn2per12 = _mm_set1_pd(mRange * ln2per12);
__m128d minLn2per12 = _mm_set1_pd(mMin * ln2per12);
__m128d loaded_a = _mm_load_pd(pA);
__m128d loaded_b = _mm_load_pd(pB);
__m128d result = _mm_add_pd(loaded_a, loaded_b);
result = _mm_max_pd(bound_lower, result);
result = _mm_min_pd(bound_upper, result);
result = _mm_mul_pd(rangeLn2per12, result);
result = _mm_add_pd(minLn2per12, result);
double *pCEnd = pC + roundintup8(blockSize);
for (; pC < pCEnd; pA += 8, pB += 8, pC += 8) {
_mm_store_pd(pC, result);
loaded_a = _mm_load_pd(pA + 2);
loaded_b = _mm_load_pd(pB + 2);
result = _mm_add_pd(loaded_a, loaded_b);
result = _mm_max_pd(bound_lower, result);
result = _mm_min_pd(bound_upper, result);
result = _mm_mul_pd(rangeLn2per12, result);
result = _mm_add_pd(minLn2per12, result);
_mm_store_pd(pC + 2, result);
loaded_a = _mm_load_pd(pA + 4);
loaded_b = _mm_load_pd(pB + 4);
result = _mm_add_pd(loaded_a, loaded_b);
result = _mm_max_pd(bound_lower, result);
result = _mm_min_pd(bound_upper, result);
result = _mm_mul_pd(rangeLn2per12, result);
result = _mm_add_pd(minLn2per12, result);
_mm_store_pd(pC + 4, result);
loaded_a = _mm_load_pd(pA + 6);
loaded_b = _mm_load_pd(pB + 6);
result = _mm_add_pd(loaded_a, loaded_b);
result = _mm_max_pd(bound_lower, result);
result = _mm_min_pd(bound_upper, result);
result = _mm_mul_pd(rangeLn2per12, result);
result = _mm_add_pd(minLn2per12, result);
_mm_store_pd(pC + 6, result);
loaded_a = _mm_load_pd(pA + 8);
loaded_b = _mm_load_pd(pB + 8);
result = _mm_add_pd(loaded_a, loaded_b);
result = _mm_max_pd(bound_lower, result);
result = _mm_min_pd(bound_upper, result);
result = _mm_mul_pd(rangeLn2per12, result);
result = _mm_add_pd(minLn2per12, result);
}
И я бы сказал, что это работает довольно хорошо. НО, не могу найти exp функция для SSE2, чтобы завершить цепочку операций.
чтение этот, кажется мне нужно назвать стандартным exp() из библиотеки?
В самом деле? Разве это не наказывает? Есть ли другие способы? Отличная встроенная функция?
Я на MSVC, /arch:SSE2, /O2, производящий 32-битный код.
Решение
Существует несколько библиотек, которые обеспечивают экспоненциальную векторизацию с большей или меньшей точностью.
- SVML, поставляется с компилятором Intel (он также предоставляет встроенные функции, поэтому, если у вас есть лицензия, вы можете использовать ее), имеет другой уровень точности (и скорости)
- ты упомянул IPP, также от Intel, которые также предоставляют некоторую функциональность
- MKL также предоставляет некоторый интерфейс для этого вычисления (для этого исправление ISA может быть сделано с помощью макросов, например, если вам нужна воспроизводимость или точность)
- fmath это еще один вариант, вы можете оторвать код из векторизованного опыта, чтобы интегрировать его в ваш цикл.
По опыту, все это быстрее и точнее, чем пользовательское приближение падде (даже не говоря о нестабильном расширении Тейлора, которое ОЧЕНЬ быстро даст вам отрицательное число).
Для SVML, IPP и MKL я бы проверил, какой из них лучше: вызов изнутри вашего цикла или вызов exp с одним вызовом для вашего полного массива (поскольку библиотеки могут использовать AVX512 вместо просто SSE2).
Другие решения
Самый простой способ — использовать аппроксимацию экспоненты. Один возможный случай, основанный на этом пределе
За n = 256 = 2^8:
__m128d fastExp1(__m128d x)
{
__m128d ret = _mm_mul_pd(_mm_set1_pd(1.0 / 256), x);
ret = _mm_add_pd(_mm_set1_pd(1.0), ret);
ret = _mm_mul_pd(ret, ret);
ret = _mm_mul_pd(ret, ret);
ret = _mm_mul_pd(ret, ret);
ret = _mm_mul_pd(ret, ret);
ret = _mm_mul_pd(ret, ret);
ret = _mm_mul_pd(ret, ret);
ret = _mm_mul_pd(ret, ret);
ret = _mm_mul_pd(ret, ret);
return ret;
}
Другая идея — полиномиальное расширение. В частности, расширение ряда Тейлора:
__m128d fastExp2(__m128d x)
{
const __m128d a0 = _mm_set1_pd(1.0);
const __m128d a1 = _mm_set1_pd(1.0);
const __m128d a2 = _mm_set1_pd(1.0 / 2);
const __m128d a3 = _mm_set1_pd(1.0 / 2 / 3);
const __m128d a4 = _mm_set1_pd(1.0 / 2 / 3 / 4);
const __m128d a5 = _mm_set1_pd(1.0 / 2 / 3 / 4 / 5);
const __m128d a6 = _mm_set1_pd(1.0 / 2 / 3 / 4 / 5 / 6);
const __m128d a7 = _mm_set1_pd(1.0 / 2 / 3 / 4 / 5 / 6 / 7);
__m128d ret = _mm_fmadd_pd(a7, x, a6);
ret = _mm_fmadd_pd(ret, x, a5);
// If fma extention is not present use
// ret = _mm_add_pd(_mm_mul_pd(ret, x), a5);
ret = _mm_fmadd_pd(ret, x, a4);
ret = _mm_fmadd_pd(ret, x, a3);
ret = _mm_fmadd_pd(ret, x, a2);
ret = _mm_fmadd_pd(ret, x, a1);
ret = _mm_fmadd_pd(ret, x, a0);
return ret;
}
Обратите внимание, что с тем же числом членов расширения вы можете получить лучшее приближение, если вы приближаете функцию для определенного диапазона x, используя, например, метод наименьших квадратов.
Все эти методы работают в очень ограниченный диапазон х но с непрерывными производными, которые могут быть важны в некоторых случаях.
Есть трюк, чтобы приблизить показатель в очень широкий ассортимент но с заметным кусочно-линейный регионы. Он основан на реинтерпретации целых чисел как чисел с плавающей точкой. Для более точного описания я рекомендую следующие ссылки:
Кусочно-линейное приближение к экспоненте и логарифму
Быстрое, компактное приближение экспоненциальной функции
Возможная реализация этого подхода:
__m128d fastExp3(__m128d x)
{
const __m128d a = _mm_set1_pd(1.0 / M_LN2);
const __m128d b = _mm_set1_pd(3 * 1024.0 - 1.05);
__m128d t = _mm_fmadd_pd(x, a, b);
return _mm_castsi128_pd(_mm_slli_epi64(_mm_castpd_si128(t), 11));
}
Несмотря на простоту и ширину x Диапазон для этого метода, будьте осторожны при использовании в математике. В небольших областях это дает кусочную аппроксимацию, которая может нарушить чувствительные алгоритмы, особенно те, которые используют дифференцирование.
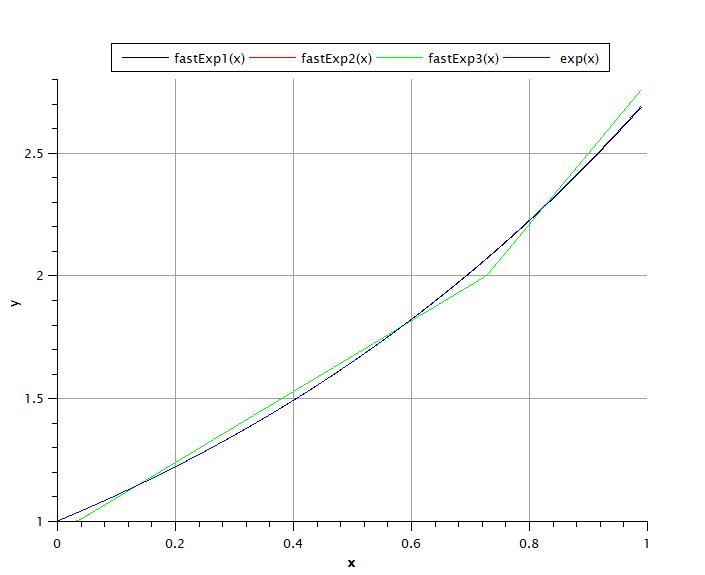
Чтобы сравнить точность разных методов, посмотрите на графику. Первый график сделан для диапазона x = [0..1). Как видите, наилучшее приближение в этом случае дает метод fastExp2(x), немного хуже, но приемлемо fastExp1(x), Худшее приближение дает fastExp3(x) — кусочная структура заметна, разрывы первой производной есть наличие.
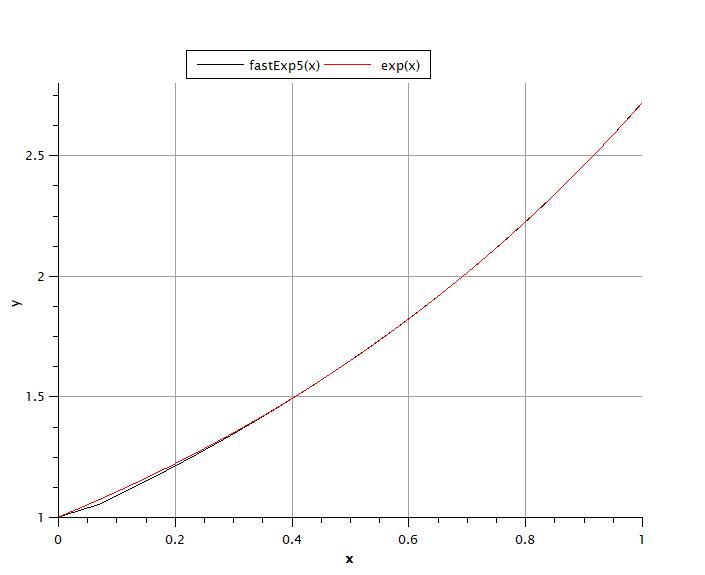
В диапазоне х = [0..10) fastExp3(x) метод обеспечивает наилучшее приближение, чуть хуже приближение fastExp1(x) — при одинаковом количестве вычислений он обеспечивает больше порядка, чем fastExp2(x),
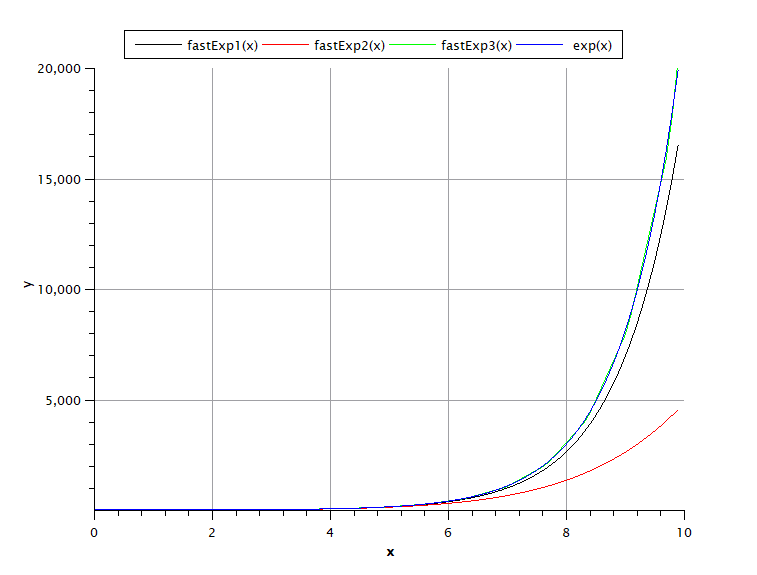
Следующим шагом является повышение точности fastExp3(x) алгоритм. Самый простой способ значительно повысить точность — использовать равенство exp(x) = exp(x/2)/exp(-x/2) Хотя это увеличивает объем вычислений, оно значительно уменьшает ошибку из-за взаимной компенсации при делении. Еще большей точности можно достичь, комбинируя методы из fastExp1(x) или же fastExp2(x) а также fastExp3(x) алгоритмы.
__m128d fastExp4(__m128d x)
{
const __m128d ap = _mm_set1_pd(0.5 / M_LN2);
const __m128d an = _mm_set1_pd(-0.5 / M_LN2);
const __m128d b = _mm_set1_pd(3 * 1024.0 - 1.05);
__m128d tp = _mm_fmadd_pd(x, ap, b);
__m128d tn = _mm_fmadd_pd(x, an, b);
tp = _mm_castsi128_pd(_mm_slli_epi64(_mm_castpd_si128(tp), 11));
tn = _mm_castsi128_pd(_mm_slli_epi64(_mm_castpd_si128(tn), 11));
return _mm_div_pd(tp, tn);
}
Реализация exp в SSE2 отсутствует, поэтому, если вы не хотите создавать свои собственные, как предложено выше, одним из вариантов является использование инструкций AVX512 на некоторых аппаратных средствах, которые поддерживают ERI (экспоненциальные и взаимные инструкции). Увидеть https://en.wikipedia.org/wiki/AVX-512#New_instructions_in_AVX-512_exponential_and_reciprocal
Я думаю, что в настоящее время это ограничивает вас фи Xeon (как указал Питер Кордес — я нашел одно утверждение о том, что это на Skylake и Cannonlake, но не могу подтвердить это), и имейте в виду, что код не будет работать на всех (то есть потерпит крах) на других архитектурах.