Как рассчитать n-й элемент этой последовательности за время log (n) или лучше?
1 4 10 22 45 88 167
Эта последовательность представляет собой свертку чисел Фибоначчи с самими собой.
Повторение
a[n] = a[n-1] + a[n-2] + Fibonacci[n+2]
Если вы предполагаете, что последовательность Фибоначчи начинается с 0,1,1,2,3,5 ... (http://oeis.org/A213587)
Как я могу сгенерировать это логарифмическое время или быстрее?
Обратите внимание, что это не домашняя работа и не проблема конкурса. Я работаю над последовательностями Фибоначчи.
Решение
Вот закрытая формула и как таковая почти гарантированно будет O(1) (рассчитано с использованием Mathematica)
вход:
RSolve[{a[n] == a[n - 2] + a[n - 1] + Fibonacci[n + 2], a[1] == 1, a[2] == 4}, a[n], n]
Выход (нажмите Вот для полного размера):
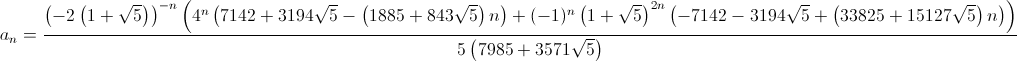
Вам нужно будет использовать некоторую арифметику с плавающей точкой, но вы все равно сможете получить большую точность от двойного типа данных. Если точность является проблемой, используйте GMP или другую библиотеку произвольной точности.
Другие решения
Это не фактический ответ на вопрос, а просто подход к генерации всей последовательности в O(n)
При условии, что вы имеете в виду O(log(n)) сложность времени для расчета только n-го элемента, а не всех до n это на самом деле довольно легко. Если вы перебираете, вы можете легко сделать O(1) для каждого элемента с надлежащей памятки.
Я предполагаю это:
a[1] = 1, a[2] = 1, fib[1] = 0, fib[2] = 1, fib[3] = 1
Тогда просто повторяй и запоминай a[n-1] а также a[n-2] так же как fib[n-1] а также fib[n-2] по пути:
long an_1 = 1; // a[2]
long an_2 = 1; // a[1]
long fib_1 = 2; // fib[4]
long fib_2 = 1; // fib[3]
// Starts with a[3]
while (true)
{
long fib = fib_1 + fib_2;
long an = an_1 + an_2 + fib;
std::cout << an;
fib_2 = fib_1;
fib_1 = fib;
an_2 = an_1;
an_1 = an;
}
редактировать: это называется амортизируемая сложность. Вычисления до n-ый элемент требует O(n) шаги, но, как у вас есть все элементы из 1 в n доступны, когда вы достигнете этой точки, стоимость вычисления каждого элемента O(1), Формальное доказательство немного сложнее, но это идея.
Я смог решить эту проблему в log n раз, преобразовав рекуррентное отношение в свертку Фибоначчи. В конце концов, рекуррентное отношение содержало только число Лукаса и число Фибоначчи. Так что я смог решить его в 2 * log n .I напишу здесь все доказательства, как только я пойму, как писать здесь математические символы.
