Как работает этот код для алгоритма MST Крускала?
Ниже приведен код C ++ для Алгоритм Крускала для поиска минимальной стоимости связующего дерева графа, заданного моим инструктором.
Я плохо понял код. Я хочу точно знать, какая часть кода проверяет формирование цикла в растущем лесу включенных ребер.
Я также хочу знать, что именно является целью parent[] массив.
Кроме того, это лучший способ, чем проверка циклов с помощью ДФС (глубина первого поиска)?
Вот код:
#include<stdio.h>
#include<stdlib.h>
int i, j, k, a, b, u, v, n, ne = 1;
int min, mincost = 0, cost[9][9], parent[9];
int find(int);
int uni(int, int);
int main()
{
printf("\n\tImplementation of Kruskal's algorithm\n");
printf("\nEnter the no. of vertices:");
scanf("%d",&n);
printf("\nEnter the cost adjacency matrix:\n");
for (i = 1; i <= n; i++)
{
for(j = 1; j <= n; j++)
{
scanf("%d",&cost[i][j]);
if(cost[i][j] == 0)
cost[i][j] = 999;
}
}
printf("The edges of Minimum Cost Spanning Tree are\n");
while(ne < n)
{
for(i = 1, min = 999; i <= n; i++)
{
for(j = 1; j <= n; j++)
{
if(cost[i][j] < min)
{
min = cost[i][j];
a = u = i;
b = v = j;
}
}
}
u = find(u);
v = find(v);
if(uni(u,v))
{
printf("%d edge (%d, %d) =%d\n", ne++, a, b, min);
mincost += min;
}
cost[a][b] = 999;
}
printf("\n\tMinimum cost = %d\n",mincost);
}
int find(int i)
{
while(parent[i])
i = parent[i];
return i;
}
int uni(int i,int j)
{
if(i!=j)
{
parent[j]=i;
return 1;
}
return 0;
}
Замечания:
Я знаю, что код немного испортился, и пользовательский ввод приведет к сбою в случае, если пользователь вводит значение больше, чем 9, но я не хочу концентрироваться на этой части, не понимая, как она работает. Я просто знаю, что он выбирает минимальный край стоимости, проверяет его на формирование цикла и затем устанавливает его значение в бесконечность (здесь 999). Я не знаю, как и где он проверяет формирование цикла. Пожалуйста, помогите, объяснив.
Решение
Код внутри while зациклиться main находит самый легкий край, который еще не был рассмотрен. Этот край находится между узлами u а также v, Край может образовывать цикл только если u а также v уже принадлежат тому же дереву.
Это:
u=find(u);
v=find(v);
находит корни деревьев, к которым u а также v принадлежат. затем main передает эти два корня uni:
if(uni(u,v))
...
int uni(int i,int j)
{
if(i!=j)
{
parent[j]=i;
return 1;
}
return 0;
}
Если два корня одинаковы, код ничего не делает, край не используется.
Другие решения
Я хочу точно знать, какая часть кода проверяет формирование цикла в растущем лесу включенных ребер. Я также хочу знать, что именно является целью массива parent [].
Кажется, вы понимаете общую идею алгоритма Крускала, но не некоторые из более важных деталей. В частности, я должен предположить, что вы не понимаете центральное и существенное использование «непересекающийся набор» (a.k.a. «set union» и другие имена) структура данных в этом алгоритме. Ибо если бы вы это сделали, вы бы наверняка поняли, что в вашем коде именно эту роль выполняет parent массив. Даже если вы не угадали из названия, find() а также uni() функции — пустая распродажа.
Код использует структуру непересекающихся множеств, чтобы отслеживать, какие группы вершин соединены ребрами, добавленными к графу. find() функция определяет, к какому набору принадлежит данная вершина, и ребра-кандидаты отклоняются, если две вершины принадлежат одному и тому же набору. uni() Функция объединяет два набора в один, когда два подграфа объединяются путем принятия ребра.
Кроме того, это лучший способ, чем проверка циклов с использованием DFS (поиск в глубину)?
Детали производительности в некоторой степени зависят от реализации несвязанного множества. Один из них особенно прост, но более сложные могут уменьшить амортизированную стоимость поисков, что приведет к повышению производительности алгоритма в целом, чем может быть достигнуто при использовании DFS.
Хорошо. Прежде чем приступить к объяснению, не стесняйтесь взять секунду и прочитать этот великолепно написанный учебник по Алгоритму Крускала на HackerEarth, так что у вас есть общее представление о том, что искать.
Теперь что касается алгоритма:
Примечание: прежде всего игнорируйте первые три строки, просто посмотрите на код в main и предположите, что все переменные объявлены заранее.
Теперь давайте начнем:
printf("\n\tImplementation of Kruskal's algorithm\n");
printf("\nEnter the no. of vertices:");
scanf("%d",&n);
printf("\nEnter the cost adjacency matrix:\n");
for(i=1;i<=n;i++)
{
for(j=1;j<=n;j++)
{
scanf("%d",&cost[i][j]);
if(cost[i][j]==0)
cost[i][j]=999;
}
}
Эти первые строки запрашивают количество вершин и матрицу смежности со стоимостью каждой вершины по отношению к любой другой вершине. Также выглядит так, что, когда нет двух ребер, соединяющих две вершины, стоимость устанавливается равной 999, чтобы код не ошибался при значении 0.
Вот как выглядит матрица смежности.
Предположим, что ваш график выглядит так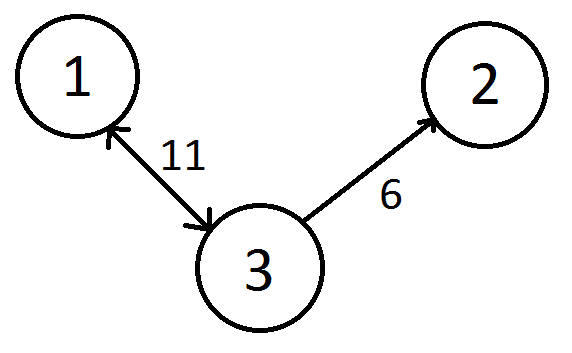
Матрица смежности будет следующей:
1 2 3
_________
1| 0 0 11
2| 0 0 0
3| 11 6 0
Это означает, что 1 связан с 3 со стоимостью 11. 2 не связан ни с одной вершиной, а 3 связан с 1 со стоимостью 11 и со 2 со стоимостью 6. Приведенный выше код изменит вышеуказанную матрицу на:
1 2 3
_____________
1| 999 999 11
2| 999 999 999
3| 11 6 999
Так что алгоритм не выбирает 0 как минимальную стоимость. И избегает выбора не связанных вершин.
После этого имеем:
printf("The edges of Minimum Cost Spanning Tree are\n");
while(ne < n)
{
for(i=1,min=999;i<=n;i++)
{
for(j=1;j <= n;j++)
{
if(cost[i][j] < min)
{
min=cost[i][j];
a=u=i;
b=v=j;
}
}
}
u=find(u);
v=find(v);
if(uni(u,v))
{
printf("%d edge (%d,%d) =%d\n",ne++,a,b,min);
mincost +=min;
}
cost[a][b]=999;
}
printf("\n\tMinimum cost = %d\n",mincost);
Во-первых, вы должны знать, что алгоритм Kruskal использует Connected Components, чтобы выяснить, связаны ли 2 вершины или нет (это также причина, по которой алгоритм Kruskal не создает круги). Итак, давайте, что делает код.
for(i=1,min=999;i<=n;i++)
{
for(j=1;j <= n;j++)
{
if(cost[i][j] < min)
{
min=cost[i][j];
a=u=i;
b=v=j;
}
}
}
Это несколько прямо вперед. То, что он делает, проходит через матрицу и находит в ней наименьшее значение. Так что для примера, который я привел, сначала нужно найти 6.
Так min = 6, u = 3 (начальная вершина), v = 2 (конечная вершина). Так что теперь, чтобы понять, что последует, вам нужно ПРОЧИТАТЬ о непересекающихся множествах и связанных компонентах. К счастью для вас, на HackerEarth снова есть 10-минутное руководство по чтению, которое поможет вам понять, как работают Подключенные компоненты. Вы можете найти это Вот.
Итак, вот что происходит. Алгоритм говорит, что наименьшая стоимость сейчас составляет 3-> 2, что стоит 6. Давайте добавим это к графику, который мы строим на фоне со связанными компонентами, и установим стоимость на 999, чтобы мы не пересматривали ее. Так вот: u=find(u);
Идет в родительский массив и проверяет в позиции 3 (arr[3]) кто родитель? Ответ 3, так как мы еще не подключили его к любому другому компоненту. Далее он делает то же самое для 2 (arr[2]), который также остается прежним, так как мы не подключили его. На что-нибудь еще. И затем объединяет их в один. То есть массив теперь становится:
[1, 2, 3] -> [1, 3, 3] (minCost is now equal to 6)
Затем это добавляет мин к minCost, который является ответом. И изменяет стоимость с 3-> 2 до 999, чтобы мы не пересматривали ее.
Это повторяет этот процесс, так что мы имеем:
// min=6, u=3, v=2
[1, 2, 3] -> [1, 3, 3] // minCost = 6
// min=11, u=1, v=3
[1, 3, 3] -> [1, 3, 1] // minCost = 17
// min=11, u=3, v=1 !!! CAREFUL NOW
Moving over to
parent of parent[3] == parent[1] meaning that they have the same parent so they are CONNECTED.
if(uni(u,v)) <-- This won't run since uni(3, 1) will return 0 meaning that they are connected so the min won't be added to minCost this time.
И на этом алгоритм заканчивается. Он печатает окончательную стоимость 17, и все готово. Переменная ne используется только как счетчик, чтобы облегчить понимание распечаток.
Я надеюсь, это поможет вам. Обязательно прочитайте учебники, которые я связал, они действительно помогут вам понять логику, потому что Алгоритм Чудесного Крускала.
Ссылки, упомянутые выше:
Алгоритм Крускала: https://www.hackerearth.com/practice/algorithms/graphs/minimum-spanning-tree/tutorial/
Подключенные компоненты: https://www.hackerearth.com/practice/data-structures/disjoint-data-strutures/basics-of-disjoint-data-structures/tutorial/
