Как работает gluLookAt?
Из моего понимания,
gluLookAt(
eye_x, eye_y, eye_z,
center_x, center_y, center_z,
up_x, up_y, up_z
);
эквивалентно:
glRotatef(B, 0.0, 0.0, 1.0);
glRotatef(A, wx, wy, wz);
glTranslatef(-eye_x, -eye_y, -eye_z);
Но когда я распечатаю ModelView матрица, призыв к glTranslatef() кажется, не работает должным образом. Вот фрагмент кода:
#include <stdlib.h>
#include <stdio.h>
#include <GL/glut.h>
#include <iomanip>
#include <iostream>
#include <string>
using namespace std;
static const int Rx = 0;
static const int Ry = 1;
static const int Rz = 2;
static const int Ux = 4;
static const int Uy = 5;
static const int Uz = 6;
static const int Ax = 8;
static const int Ay = 9;
static const int Az = 10;
static const int Tx = 12;
static const int Ty = 13;
static const int Tz = 14;
void init() {
glClearColor(0.0, 0.0, 0.0, 0.0);
glEnable(GL_DEPTH_TEST);
glShadeModel(GL_SMOOTH);
glEnable(GL_LIGHTING);
glEnable(GL_LIGHT0);
GLfloat lmodel_ambient[] = { 0.8, 0.0, 0.0, 0.0 };
glLightModelfv(GL_LIGHT_MODEL_AMBIENT, lmodel_ambient);
}
void displayModelviewMatrix(float MV[16]) {
int SPACING = 12;
cout << left;
cout << "\tMODELVIEW MATRIX\n";
cout << "--------------------------------------------------" << endl;
cout << setw(SPACING) << "R" << setw(SPACING) << "U" << setw(SPACING) << "A" << setw(SPACING) << "T" << endl;
cout << "--------------------------------------------------" << endl;
cout << setw(SPACING) << MV[Rx] << setw(SPACING) << MV[Ux] << setw(SPACING) << MV[Ax] << setw(SPACING) << MV[Tx] << endl;
cout << setw(SPACING) << MV[Ry] << setw(SPACING) << MV[Uy] << setw(SPACING) << MV[Ay] << setw(SPACING) << MV[Ty] << endl;
cout << setw(SPACING) << MV[Rz] << setw(SPACING) << MV[Uz] << setw(SPACING) << MV[Az] << setw(SPACING) << MV[Tz] << endl;
cout << setw(SPACING) << MV[3] << setw(SPACING) << MV[7] << setw(SPACING) << MV[11] << setw(SPACING) << MV[15] << endl;
cout << "--------------------------------------------------" << endl;
cout << endl;
}
void reshape(int w, int h) {
float ratio = static_cast<float>(w)/h;
glViewport(0, 0, w, h);
glMatrixMode(GL_PROJECTION);
glLoadIdentity();
gluPerspective(45.0, ratio, 1.0, 425.0);
}
void draw() {
float m[16];
glClear(GL_COLOR_BUFFER_BIT | GL_DEPTH_BUFFER_BIT);
glMatrixMode(GL_MODELVIEW);
glLoadIdentity();
glGetFloatv(GL_MODELVIEW_MATRIX, m);
gluLookAt(
300.0f, 0.0f, 0.0f,
0.0f, 0.0f, 0.0f,
0.0f, 1.0f, 0.0f
);
glColor3f(1.0, 0.0, 0.0);
glutSolidCube(100.0);
glGetFloatv(GL_MODELVIEW_MATRIX, m);
displayModelviewMatrix(m);
glutSwapBuffers();
}int main(int argc, char** argv) {
glutInit(&argc, argv);
glutInitDisplayMode(GLUT_DOUBLE | GLUT_RGB | GLUT_DEPTH);
glutInitWindowSize(400, 400);
glutInitWindowPosition(100, 100);
glutCreateWindow("Demo");
glutReshapeFunc(reshape);
glutDisplayFunc(draw);
init();
glutMainLoop();
return 0;
}
Независимо от того, какое значение я использую для eye вектор:
300, 0, 0 или же
0, 300, 0 или же
0, 0, 300
вектор перевода такой же, что не имеет никакого смысла, потому что порядок кода в обратном порядке, так glTranslatef должен бежать сначала, затем 2 вращения. Кроме того, матрица вращения полностью независима от столбца перевода (в матрице ModelView), что может вызвать это странное поведение?
Вот вывод с вектором глаза (0.0f, 300.0f, 0.0f)
MODELVIEW MATRIX
--------------------------------------------------
R U A T
--------------------------------------------------
0 0 0 0
0 0 0 0
0 1 0 -300
0 0 0 1
--------------------------------------------------
Я бы ожидал T столбец будет (0, -300, 0)! Так может кто-нибудь помочь мне объяснить это?
Реализация gluLookAt от http://www.mesa3d.org
void GLAPIENTRY
gluLookAt(GLdouble eyex, GLdouble eyey, GLdouble eyez, GLdouble centerx,
GLdouble centery, GLdouble centerz, GLdouble upx, GLdouble upy,
GLdouble upz)
{
float forward[3], side[3], up[3];
GLfloat m[4][4];
forward[0] = centerx - eyex;
forward[1] = centery - eyey;
forward[2] = centerz - eyez;
up[0] = upx;
up[1] = upy;
up[2] = upz;
normalize(forward);
/* Side = forward x up */
cross(forward, up, side);
normalize(side);
/* Recompute up as: up = side x forward */
cross(side, forward, up);
__gluMakeIdentityf(&m[0][0]);
m[0][0] = side[0];
m[1][0] = side[1];
m[2][0] = side[2];
m[0][1] = up[0];
m[1][1] = up[1];
m[2][1] = up[2];
m[0][2] = -forward[0];
m[1][2] = -forward[1];
m[2][2] = -forward[2];
glMultMatrixf(&m[0][0]);
glTranslated(-eyex, -eyey, -eyez);
}
Решение
Если мы позволим матрицу вращения и перевода, как ваша матрица просмотра модели
Rxx Rxy Rxz Tx
Ryx Ryy Ryz Ty
Rzx Rzy Rzz Tz
0 0 0 1
действовать на произвольный вектор
x
y
z
1
мы получаем
Rxx x + Rxy y + Rxz z + Tx
Ryx x + Ryy y + Ryz z + Ty
Rzx x + Rzy y + Rzz z + Tz
1
(Я пишу вещи так, чтобы векторы умножались на матрицы слева).
Это показывает, что компоненты перевода матрицы дают перевод для применения после делает вращение. Вот почему они не совпадают с вашим вектором (-eye_x, -eye_y, -eye_z), потому что, как вы указали, перевод выполняется перед вращением.
Причина, по которой перевод всегда выполняется в направлении -z, заключается в том, что в окне просмотра направление -z указывает на центр. Поскольку у вас всегда есть центры на 300 единиц от глаза, все ваши позиции глаза помещают центр в (0, 0, -300) в рамке обзора. Следовательно, поскольку центр начинается в начале координат до того, как мы выполним какой-либо перевод, перевод, чтобы дать ему правильные координаты, должен быть (0, 0, -300).
Кроме того, вы могли заметить это, но матрица вида модели, которую вы показываете, является патологической, потому что у вас есть вектор вверх, указывающий вдоль направления просмотра (от глаза к центру). Это объясняет, почему у него есть два полных ряда нулей.
Другие решения
«Я очень озадачен тем, как в этом коде выполняются повороты с использованием векторов прямого, восходящего и бокового векторов …» Я думаю, вы должны кое-что знать о «камере UVN». Существует некоторая теория о преобразованиях координат между двумя системами координат. .В приведенном выше примере две координаты — это мировые координаты и координаты камеры.
И результат:
Икс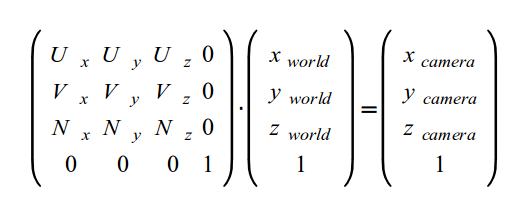
N — вектор от цели к камере. Также известный как вектор «взгляд на» в некоторой трехмерной литературе. Этот вектор соответствует оси -Z.
V — В вертикальном положении это вектор от вашей головы к небу. Если вы пишете симулятор полета и самолет переворачивается, этот вектор вполне может указывать на землю. Этот вектор соответствует оси Y.
U — этот вектор направлен от камеры к «правой» стороне »и соответствует оси X.
@ Andon M. Coleman — насколько важна приведенная выше строка диаграммы?
Наличие основной матрицы строк или столбцов относится к представлению в памяти 2D-структур в 1D-памяти и не имеет ничего общего с приведенной выше диаграммой матрицы преобразования 4×4.
Если бы векторы U, V, N были записаны в виде столбцов, как вы предполагаете, то у вас была бы трансформация пространства камеры в мир.
Тем не менее, вход в матрицу является позицией в мировом пространстве, а выход — в положении камеры и, следовательно, матрица представляет собой трансформацию мирового пространства в пространство камеры.
Причина, по которой U, V, N транспонируются, заключается в том, что это обратная матрица, которую вы предлагаете, и с помощью свойства ортогональных матриц, где их обратная также является транспонированием. То есть, мы записываем векторы U, V, N в строки, чтобы получить преобразование пространства мира в пространство камеры, а столбцы U, V, N — в преобразование пространства камеры в пространство мира.
Кроме того, выбор умножения на мировую позицию справа обусловлен тем, что на диаграмме используются векторы столбцов. Мы бы оставили множитель, если бы мы использовали векторы строк. Это НИЧЕГО не связано с тем, как мы сохраняем матрицу в памяти, и имеет все, что связано с тем, как мы умножаем две матрицы вместе, то есть, преобразуем ли мы наш вектор в матрицу 1X4 или 4X1, прежде чем умножить ее на матрицу 4×4.
Короче говоря, приведенная выше диаграмма — это хорошо, это просто преобразование из одного пространства в другое, пожалуйста, не путайте этот вопрос с разговором о расположении памяти, который является деталью программирования.
