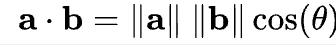Как проверить, направлены ли векторы в одном направлении

Формула, которую вы включаете (и которая содержит ошибку — продукт «*», а не «* =»), дает вам сущность движения — длину вектора. Что вы уже знаете, так как это единица измерения вектор и, следовательно, имеет длину 1.

Вам нужно вместо этого выполнить скалярное произведение между двумя векторами. Вы получаете 1, если два единичных вектора полностью выровнены (параллельные), -1, если они антипараллельны, и ноль, если они нормальны друг к другу.

«Больше севера, чем юга» означает, что скалярное произведение положительно, поэтому:

вернитесь, если они смотрят на север с юга

Alignment =  ((PlayerVector.x * NorthVector.x)
+ (PlayerVector.y * NorthVector.y)
+ (PlayerVector.z * NorthVector.z));

return (Alignment > 0);

Что если бы я хотел сказать, обращено ли оно на восток / запад?

Точечный продукт говорит вам сколько двух векторов выровнено. Это та же формула, показанная Кевином Глассоном, без норм единичных векторов, поскольку они равны 1, а деление на единицу ничего не меняет.

Таким образом, вы не можете использовать его, чтобы сказать, где находится вектор кроме как с точки зрения другого вектора. И именно поэтому вам дан северный вектор; с одним вектором игрока вы не можете запустить скалярное произведение. Чтобы узнать, смотрит ли игрок на восток, вам нужен вектор восток (или вектор запад, а затем взять противоположный знак).

Так что, если число вернется, скажем, 35, это означает, что оно обращено больше на север, чем на юг, но почему?

Почему это так: вы можете найти объяснение на странице Википедии, скалярное произведение равно произведению двух длин на косинус их угла. Поскольку длины равны 1, это просто косинус. Косинус варьируется от 1 до -1 (поэтому вы не можете получить 35). Когда косинус равен 1, это означает, что угол равен нулю и векторы выровнены; когда это -1, они противоположны. Косинус нуля означает, что векторы нормальны друг к другу, то есть образуют угол 90 °, и в этом случае это означает, что игрок обращен или Восток, Запад или Вверх или Вниз — но это не говорит вам который.

Я думаю, что будет работать, принимая ‘скалярное произведение’ векторов. Используя следующую форму:

Где бы вы перестроили тета. Это даст вам угол между двумя векторами.

По моему мнению, по крайней мере, если угол был равен 0, то вы указываете точно на север, а если угол был больше 90, то вы смотрели на юг.

Я не знаю точно, как вы собираетесь использовать это, но это должно сработать для возможности отличить север от юга в трехмерном пространстве.

Ну, вы можете использовать точечное произведение, чтобы получить угол между 2 векторами. Формула следующая:

cos(phi) = (a * b) / (|a|*|b|)

Что превращает в это:

phi = acos((ax*bx + ay*by + az * bz) / (sqrt(ax^2 + ay^2 + az^2)+sqrt(bx^2 + by^2 + bz^2)))

Теперь скалярное произведение симметрично, что означает: (1,1,1)(2,2,2) дает тот же результат, что и (2,2,2)(1,1,1). Следовательно, вы должны добавить еще один шаг. Добавляя третий вектор, угол которого к первому заданному вектору вы знаете, вы можете проверить истинный угол между двумя векторами. Чтобы получить этот опорный вектор, можно повернуть первый вектор вокруг оси, теперь, чтобы убедиться, что он является действительным опорным, он должен находиться в той же плоскости, что и векторы a и b.
Это означает, что ваша ось, чтобы повернуть ваш первый вектор arround, должна быть ортогональной к вектору 1 и 2, векторное произведение 2 векторов дает вектор, ортогональный к обоим, поэтому мы будем использовать полученный вектор как ось.

axis = a x b

Это равно:

axis = (aybz-azby, azbx-axbz, axby-aybx)

Чтобы повернуть вектор на заданную величину вокруг оси, необходимо сделать следующее:

double R[3][3] = {};
Vector axis = Axis.getUnitVector();
double deg = degrees / 180 * M_PI;
R[0][0] = axis.X * axis.X * (1 - cos(deg)) + cos(deg); R[0][1] = axis.X * axis.Y * (1 - cos(deg)) - axis.Z * sin(deg); R[0][2] = axis.X * axis.Z * (1 - cos(deg)) + axis.Y * sin(deg);
R[1][0] = axis.Y * axis.X * (1 - cos(deg)) + axis.Z * sin(deg); R[1][1] = axis.Y * axis.Y * (1 - cos(deg)) + cos(deg); R[1][2] = axis.Y * axis.Z * (1 - cos(deg)) - axis.X * sin(deg);
R[2][0] = axis.Z * axis.X * (1 - cos(deg)) - axis.Y * sin(deg); R[2][1] = axis.Z * axis.Y * (1 - cos(deg)) + axis.X * sin(deg); R[2][2] = axis.Z * axis.Z * (1 - cos(deg)) + cos(deg);
double x = this->X * R[0][0] + this->Y * R[0][1] + this->Z * R[0][2];
double y = this->X * R[1][0] + this->Y * R[1][1] + this->Z * R[1][2];
double z = this->X * R[2][0] + this->Y * R[2][1] + this->Z * R[2][2];

Единица измерения определяется следующим образом:

e_a = (ax / sqrt(ax^2+ay^2+az^2),ay / sqrt(ax^2+ay^2+az^2),az / sqrt(ax^2+ay^2+az^2))

Используя эту новую ось, мы можем повернуть наш первый вектор на 90 °. Вычисляя угол между нашим эталоном и вторым вектором, мы теперь можем оценить реальный угол между первым и вторым вектором. Если угол к эталону больше 90 °, 2-й вектор находится в 3-м или 4-м секторе или в декартовой системе координат, то есть для получения реального угла нам нужно вычесть наш средний угол между первым и 2-м вектором из 360 °. Если угол к эталону меньше 90 °, рассчитанный угол является реальным углом.

Теперь есть другая проблема, что / где север? Если бы мы знали север, мы могли бы просто вычислить угол между севером и двумя векторами, и тот, у которого угол меньше, был бы больше к северу. Это означает, что нет причин оценивать опорный вектор или строить и применять матрицу вращения.

В случае фиксированного севера вы также можете проецировать свои векторы на плоскость, содержащую север, и упростить необходимые вычисления.
Предоставьте больше информации, и я отредактирую это.

edit: / так как вы предоставляете север и вектор игрока, просто рассчитайте угол между ними.