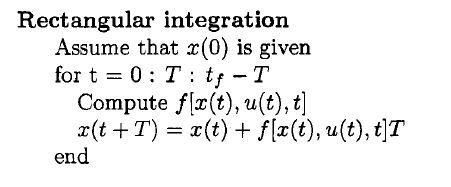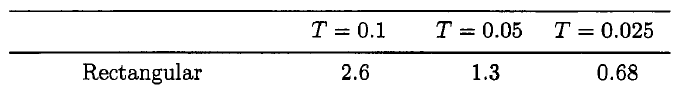Как придумать эту процентную ошибку с помощью метода прямоугольной интеграции

Question

Как придумать эту процентную ошибку с помощью метода прямоугольной интеграции

Я рассматриваю некоторые численные методы для интеграции. Я натолкнулся на метод Прямоугольной интеграции (то есть метод Эйлера). Согласно книге, которую я читаю, фактический алгоритм

Код не требует пояснений. Автор приводит этот пример dxdt=cos(t) с начальным значением x(0)=0, Аналитическое решение x=sin(t), Мы можем вычислить ошибку в t=1 и действительно, автор предоставляет это в следующей таблице:

Проблема в том, что в моем следующем коде ошибка составляет 9,1%, но в предыдущей таблице ошибка фактически составляет 2,6. Я сделал ошибку?

#include <iostream>
#include <cmath>

int main()
{
double x(0.0), dxdt, t(0.0), T(0.1), stopTime(1.0);

for ( ; t <= stopTime; t += T ){
dxdt = cos(t);
x += dxdt*T;

if ( t > 0.9 )
std::cout << "Time: " << t << "  Error: " << fabs( (x - sin(t)) /sin(t) )*100.0 <<  std::endl;
}

return 0;
}

1

c++numerical-integration numerical-methods

Решение

Другие решения

Других решений пока нет …

Источник

Accepted Answer

Вы должны принять во внимание, что пока x обновляется до приближения x(t+T)переменная цикла t будет увеличиваться только в самом конце цикла, поэтому сохраняет его значение t во время выхода. Это несоответствие времени вносит дополнительную относительную ошибку abs(sin(t+T)/sin(t)-1) который для t=1, T=0.1 около 5.91 %,

Вы также должны сделать цикл стабильным при ошибках округления в t увеличение, либо путем вычисления точного числа циклов, либо путем выбора границ в неравенстве, которые находятся между шагами, как в

while ( t < stopTime-0.5*T ){
dxdt = cos(t);
x += dxdt*T;
t += T;

if ( t > stopTime -2.5*T )
std::cout << "Time: " << t << "  Error: " << fabs( (x - sin(t)) /sin(t) )*100.0 <<  std::endl;

}

1