Как преобразовать точки, назначенные твердому телу вдоль стороны тела?
Чтобы описать проблему, я привожу пример здесь на рисунке ниже.
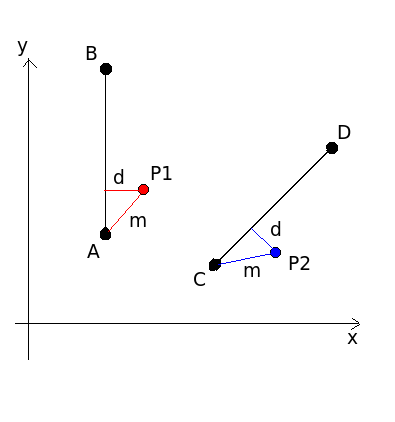
Как видно, есть линия AB и назначенная ей точка p1.
Для этой строки у меня есть соответствующая строка, а именно CD. Я ищу координату точки p2. Соотношение между точкой p2 и линией CD должно быть таким же, как отношение между точкой p1 и линией AB (одинаковое расстояние d и одинаковая длина m). У меня есть координаты точек A, B, p1, C, D, и я ищу p2. В общем, d и m могут принять масштабный коэффициент для линии CD и точки p2, что мы уже знаем.
Как вы, возможно, знаете, у этой проблемы есть другое ложное решение, такое как p3 в левой части строки CD, чего мы должны избегать.
В моей реальной задаче у меня есть 10 линий AB и около 500 точек, таких как p1, расположенных на разных линиях AB. У меня есть десять соответствующих строк CD, я ищу 500 соответствующих точек p2.
Используя алгебру и геометрию, можно решить проблему, но я ищу быстрый и эффективный метод для реализации на C ++.
Большое спасибо за ваши комментарии и предложения.
Решение
Прежде всего, вам нужно представить любое движение AB в виде поворота и перемещения относительно одной точки, например точки A, для простоты. Затем для любой другой точки, которую необходимо повернуть вместе с AB, вы должны переместить эту точку в пространство линии AB, вычтя точку A, а затем преобразовать ее обратно в мировое пространство, добавив новую точку A обратно после перевода и вращение.
У меня нет формулы под рукой, но я попытаюсь найти пример.
РЕДАКТИРОВАТЬ
Непроверенный код:
void transform_points(const point2f ¢er, vector<point2f> &points, const point2f &offset, float angle)
{
// transform points into a space where 'center' is the origin
mat3f to_origin = mat3f(1, 0, -center.x,
0, 1, -center.y,
0, 0, 1);
// rotate the points around the origin
mat3f rot = mat3f(cos(angle), -sin(angle), 0,
sin(angle), cos(angle), 0,
0, 0, 1);
// move the points back into world space
mat3f to_world = mat3f(1, 0, center.x,
0, 1, center.y,
0, 0, 1);
// offset the points by 'offset'
mat3f off = mat3f(1, 0, offset.x,
0, 1, offset.y,
0, 0, 1);
// concatenate all transformations for efficiency
mat3f xform = off * to_world * rot * to_origin;
// this loop could be parallelized using SIMD or multiple cores
for(auto &p : points)
p = xform * p;
}
Другие решения
