Как повернуть линию вокруг одной из ее вершин
Я делаю свой первый движок лучевого вещания и хотел бы повернуть линию на угол θ
Как это сделать? Можно ли показать мне какой-нибудь базовый код C ++ или псевдокод?
Это изображение описывает мою проблему:
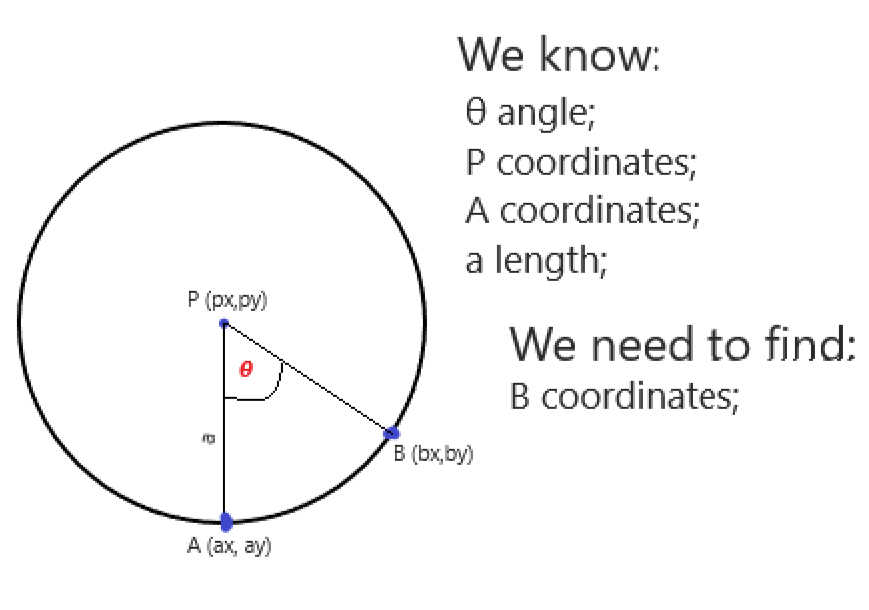
Дополнительный вопрос
Я решил сделать все это в graphics.hпотому что это самый простой графический заголовок для C / C ++.
Решение
Ты хочешь:
B = P + M * (A - P)
куда M матрица вращения 2D:
M = | cos(ϴ) -sin(ϴ) |
| sin(ϴ) cos(ϴ) |
В C ++ это можно записать так:
float c = cos(theta), s = sin(theta);
float dx = ax - px, dy = ay - py;
float bx = px + c * dx - s * dy;
float by = py + s * dx + c * dy;
Другие решения
Один простой алгоритм:
- Переместить круг
-P, чтобыPнаходится в (0, 0). - Поворот
Aна угол, умножив его на матрица вращения. - Переместить круг
Pвосстановить свое первоначальное положение.
Все эти три шага могут быть выполнены с использованием одного умножения матрицы 3х3.
Скалярное произведение двух векторов обладает следующим свойством:
vec(PA) . vec(PB) = rho cos theta
Принимая определение наших двух векторов:
vec(PA) = (x_a-x_p, y_a-y_p)
vec(PB) = (x_b-x_p, y_b-y_p)
Мы можем получить:
(x_a-x_p)(x_b-x_p) + (y_a-y_p)(y_b-y_p) = rho cos theta (1)
Так как PA = PB, мы также имеем:
(x_a-x_p)^2 + (y_a-y_p)^2 = (x_b-x_p)^2 + (y_b-y_p)^2 (2)
От (1) а также (2) вы можете получить x_bа также y_b с некоторым арифметическим автопилотом.
