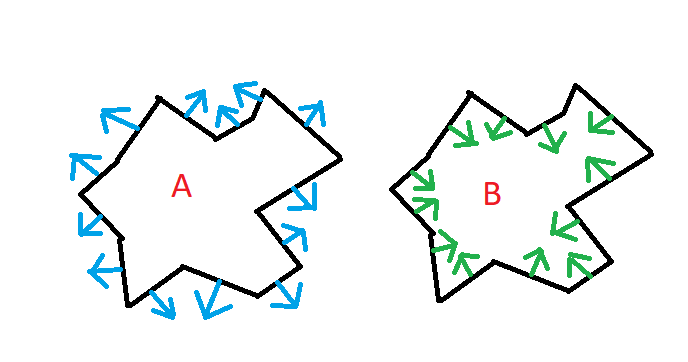
Как определить, находится ли замкнутый вогнутый многоугольник наизнанку?
У меня есть 2 полигона, А и В.
Каждый многоугольник замкнут и вогнут. С каждым ребром многоугольника связана нормаль (сине-зеленая), обращенная внутрь или наружу. Порядок намотки вершин каждого многоугольника произвольный и не связан с направлением нормалей.
Используя только нормали и вершины каждого многоугольника, как я могу определить, направлен ли периметр многоугольника наружу (A) или внутрь (B)? В идеале я ищу решение, которое не включает в себя тесты на лучевое вещание или пересечение.
Решение
Я думаю, что нашел решение, поэтому в моих тестах он всегда возвращает правильный результат.
Сначала я определяю порядок намотки многоугольника, используя метод суммы, описанный в ответе здесь:
Как определить, находится ли список точек многоугольника по часовой стрелке?
Затем я вычисляю нормали первого ребра вручную, найдя перекрестное произведение вектора направления и вектора [0,0,1], а затем нормализуя его. Так как это 2d многоугольники, [0,0,1] (где z — ось вверх) всегда будет перпендикулярна направлению любого ребра, поэтому перекрестное произведение всегда будет возвращать действительную нормаль. Затем важной частью является умножение результирующей нормали на -1, если общий многоугольник против часовой стрелки. Это даст нам постоянно обращенную наружу нормаль, независимо от порядка намотки, благодаря правилу правой руки для перекрестного произведения.
Наконец, я вычисляю точечное произведение вычисленной вручную нормали и назначенной нормали первого ребра (сине-зеленая нормали исходного изображения) … если точечное произведение> 0, наша назначенная нормаль (и, таким образом, наша многоугольник) обращен наружу, в противном случае он обращен внутрь. Это нужно сделать только для первого ребра многоугольника, так как все нормали либо наружу, либо внутрь.
Другие решения
Других решений пока нет …