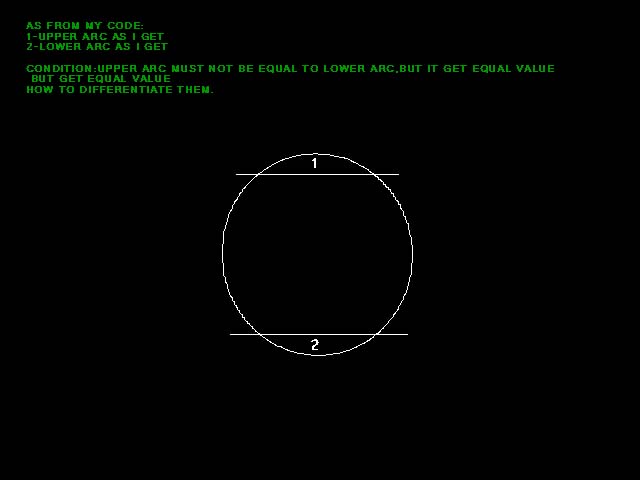
Как определить длину верхней и нижней дуги по изображению эллипса

Question

Как определить длину верхней и нижней дуги по изображению эллипса

Здесь я пытаюсь найти верхнюю и нижнюю дуги, используя векторное изображение (контуры изображений), но это не может дать результат извлечения. Предложите любой другой метод, чтобы найти верхнюю и нижнюю дугу по изображениям и их длине.

Вот мой код

    Mat image =cv::imread("thinning/20d.jpg");
int i=0,j=0,k=0,x=320;
for(int y = 0; y < image.rows; y++)
{
if(image.at<Vec3b>(Point(x, y))[0] >= 250 && image.at<Vec3b>(Point(x, y))[1] >= 250 && image.at<Vec3b>(Point(x, y))[2] >= 250){
qDebug()<<x<<y;
x1[i]=x;
y1[i]=y;
i=i+1;
}
}
for(i=0;i<=1;i++){
qDebug()<<x1[i]<<y1[i];
}
qDebug()<<"UPPER ARC";
for(int x = 0; x < image.cols; x++)
{
for(int y = 0; y <= (y1[0]+20); y++)
{
if(image.at<Vec3b>(Point(x, y))[0] >= 240 && image.at<Vec3b>(Point(x, y))[1] >= 240 && image.at<Vec3b>(Point(x, y))[2] >= 240){
x2[j]=x;
y2[j]=y;
j=j+1;
qDebug()<<x<<y;
}}
}
qDebug()<<"Lower ARC";
for(int x = 0; x < image.cols; x++)
{
for(int y = (y1[1]-20); y <= image.rows; y++)
{
if(image.at<Vec3b>(Point(x, y))[0] >= 240 && image.at<Vec3b>(Point(x, y))[1] >= 240 && image.at<Vec3b>(Point(x, y))[2] >= 240){
x3[k]=x;
y3[k]=y;
k=k+1;
qDebug()<<x<<y;
}}
}

Выше кода я получаю координаты, используя точки координат, я могу найти длину дуги, но ее несоответствие полученному результату.

Вот фактическое изображение:

Изображение1:

После прореживания я получил:

Ожидаемый результат:

1

c++ellipse image-processing opencv qt

Решение

Другие решения

Других решений пока нет …

Источник

Accepted Answer

Поскольку вы не можете определить, что именно является верхней / нижней дугой, я буду считать, что вы разрезали эллипс пополам горизонтальной линией, проходящей через среднюю точку эллипса. Если это не так, то вы должны адаптировать это самостоятельно … Хорошо, теперь, как это сделать:

бинаризованное изображение

Поскольку вы предоставляете JPG, цвета искажаются, поэтому остается больше, чем просто черный и белый
тонкая граница до 1 пикселя

Заполните внутреннюю часть белым цветом, а затем перекрасьте все белые пиксели, не соседствующие с черными пикселями, в какой-то неиспользованный или черный цвет. Есть много других вариантов, как этого добиться …
найти ограничивающую рамку

поиск по всем пикселям и запоминание мин, макс x,y координаты всех белых пикселей. Пусть зовут их x0,y0,x1,y1,
вычислительный центр эллипса

просто найдите середину ограничительной рамки
```
cx=(x0+x1)/2
cy=(y0+y1)/2
```
считать пиксели для каждой эллиптической дуги

иметь счетчик для каждой дуги и просто увеличивать счетчик верхней дуги для любого белого пикселя, который имеет y<=cy и ниже, если y>=cy, Если ваша система координат отличается, то условия могут быть обратными.
найти параметры эллипса

просто найдите белый пиксель, ближайший к (cx,cy) это будет конечная точка малой полуоси b давай называть это (bx,by), Также найдите самый дальний белый пиксель для (cx,cy) это будет главная конечная точка полуоси (ax,ay), Расстояние между ними и центром даст вам a,b и их положение, вычтенное по центру, даст вам векторы с вращением вашего эллипса. угол можно получить с помощью atan2 или использовать базисные векторы, как я. Вы можете проверить ортогональность точечным произведением. Может быть больше, чем 2 балла для ближайшего и дальнего пункта. в этом случае вы должны найти середину каждой группы для повышения точности.
Интегрируйте подогнанный эллипс

Сначала нужно найти угол, под которым точки эллипса y=cy затем интегрировать эллипс между этими двумя углами. Другая половина такая же, просто интегрировать angles + PI, Чтобы определить, какая половина это просто, вычислите точку в середине между угловым диапазоном и решите согласно y>=cy …

[Edit2] Здесь обновленный код C ++, который я сломал для этого:

    picture pic0,pic1,pic2;
// pic0 - source
// pic1 - output
float a,b,a0,a1,da,xx0,xx1,yy0,yy1,ll0,ll1;
int x,y,i,threshold=127,x0,y0,x1,y1,cx,cy,ax,ay,bx,by,aa,bb,dd,l0,l1;
pic1=pic0;
// bbox,center,recolor (white,black)
x0=pic1.xs; x1=0;
y0=pic1.ys; y1=0;
for (y=0;y<pic1.ys;y++)
for (x=0;x<pic1.xs;x++)
if (pic1.p[y][x].db[0]>=threshold)
{
if (x0>x) x0=x;
if (y0>y) y0=y;
if (x1<x) x1=x;
if (y1<y) y1=y;
pic1.p[y][x].dd=0x00FFFFFF;
} else pic1.p[y][x].dd=0x00000000;
cx=(x0+x1)/2; cy=(y0+y1)/2;
// fill inside (gray) left single pixel width border (thining)
for (y=y0;y<=y1;y++)
{
for (x=x0;x<=x1;x++) if (pic1.p[y][x].dd)
{
for (i=x1;i>=x;i--) if (pic1.p[y][i].dd)
{
for (x++;x<i;x++) pic1.p[y][x].dd=0x00202020;
break;
}
break;
}
}
for (x=x0;x<=x1;x++)
{
for (y=y0;y<=y1;y++) if (pic1.p[y][x].dd) { pic1.p[y][x].dd=0x00FFFFFF; break; }
for (y=y1;y>=y0;y--) if (pic1.p[y][x].dd) { pic1.p[y][x].dd=0x00FFFFFF; break; }
}
// find min,max radius (periaxes)
bb=pic1.xs+pic1.ys; bb*=bb; aa=0;
ax=cx; ay=cy; bx=cx; by=cy;
for (y=y0;y<=y1;y++)
for (x=x0;x<=x1;x++)
if (pic1.p[y][x].dd==0x00FFFFFF)
{
dd=((x-cx)*(x-cx))+((y-cy)*(y-cy));
if (aa<dd) { ax=x; ay=y; aa=dd; }
if (bb>dd) { bx=x; by=y; bb=dd; }
}
aa=sqrt(aa); ax-=cx; ay-=cy;
bb=sqrt(bb); bx-=cx; by-=cy;
//a=float((ax*bx)+(ay*by))/float(aa*bb);    // if (fabs(a)>zero_threshold) not perpendicular semiaxes

// separate/count upper,lower arc by horizontal line
l0=0; l1=0;
for (y=y0;y<=y1;y++)
for (x=x0;x<=x1;x++)
if (pic1.p[y][x].dd==0x00FFFFFF)
{
if (y>=cy) { l0++; pic1.p[y][x].dd=0x000000FF; } // red
if (y<=cy) { l1++; pic1.p[y][x].dd=0x00FF0000; } // blue
}
// here is just VCL/GDI info layer output so you can ignore it...

// arc separator axis
pic1.bmp->Canvas->Pen->Color=0x00808080;
pic1.bmp->Canvas->MoveTo(x0,cy);
pic1.bmp->Canvas->LineTo(x1,cy);

// draw analytical ellipse to compare
pic1.bmp->Canvas->Pen->Color=0x0000FF00;
pic1.bmp->Canvas->MoveTo(cx,cy);
pic1.bmp->Canvas->LineTo(cx+ax,cy+ay);
pic1.bmp->Canvas->MoveTo(cx,cy);
pic1.bmp->Canvas->LineTo(cx+bx,cy+by);
pic1.bmp->Canvas->Pen->Color=0x00FFFF00;
da=0.01*M_PI;   // dash step [rad]
a0=0.0;         // start
a1=2.0*M_PI;    // end
for (i=1,a=a0;i;)
{
a+=da; if (a>=a1) { a=a1; i=0; }
x=cx+(ax*cos(a))+(bx*sin(a));
y=cy+(ay*cos(a))+(by*sin(a));
pic1.bmp->Canvas->MoveTo(x,y);
a+=da; if (a>=a1) { a=a1; i=0; }
x=cx+(ax*cos(a))+(bx*sin(a));
y=cy+(ay*cos(a))+(by*sin(a));
pic1.bmp->Canvas->LineTo(x,y);
}

// integrate the arclengths from fitted ellipse
da=0.001*M_PI;      // integration step [rad] (accuracy)
// find start-end angles
ll0=M_PI; ll1=M_PI;
for (i=1,a=0.0;i;)
{
a+=da; if (a>=2.0*M_PI) { a=0.0; i=0; }
xx1=(ax*cos(a))+(bx*sin(a));
yy1=(ay*cos(a))+(by*sin(a));
b=atan2(yy1,xx1);
xx0=fabs(b-0.0); if (xx0>M_PI) xx0=2.0*M_PI-xx0;
xx1=fabs(b-M_PI);if (xx1>M_PI) xx1=2.0*M_PI-xx1;
if (ll0>xx0) { ll0=xx0; a0=a; }
if (ll1>xx1) { ll1=xx1; a1=a; }
}
// [upper half]
ll0=0.0;
xx0=cx+(ax*cos(a0))+(bx*sin(a0));
yy0=cy+(ay*cos(a0))+(by*sin(a0));
for (i=1,a=a0;i;)
{
a+=da; if (a>=a1) { a=a1; i=0; }
xx1=cx+(ax*cos(a))+(bx*sin(a));
yy1=cy+(ay*cos(a))+(by*sin(a));
// sum arc-line sizes
xx0-=xx1; xx0*=xx0;
yy0-=yy1; yy0*=yy0;
ll0+=sqrt(xx0+yy0);
//      pic1.p[int(yy1)][int(xx1)].dd=0x0000FF00; // recolor for visualy check the right arc selection
xx0=xx1; yy0=yy1;
}
// lower half
a0+=M_PI; a1+=M_PI; ll1=0.0;
xx0=cx+(ax*cos(a0))+(bx*sin(a0));
yy0=cy+(ay*cos(a0))+(by*sin(a0));
for (i=1,a=a0;i;)
{
a+=da; if (a>=a1) { a=a1; i=0; }
xx1=cx+(ax*cos(a))+(bx*sin(a));
yy1=cy+(ay*cos(a))+(by*sin(a));
// sum arc-line sizes
xx0-=xx1; xx0*=xx0;
yy0-=yy1; yy0*=yy0;
ll1+=sqrt(xx0+yy0);
//      pic1.p[int(yy1)][int(xx1)].dd=0x00FF00FF; // recolor for visualy check the right arc selection
xx0=xx1; yy0=yy1;
}
// handle if the upper/lower parts are swapped
a=a0+0.5*(a1-a0);
if ((ay*cos(a))+(by*sin(a))<0.0) { a=ll0; ll0=ll1; ll1=a; }
// info texts
pic1.bmp->Canvas->Font->Color=0x00FFFF00;
pic1.bmp->Canvas->Brush->Style=bsClear;
x=5; y=5; i=16; y-=i;
pic1.bmp->Canvas->TextOutA(x,y+=i,AnsiString().sprintf("center = (%i,%i) px",cx,cy));
pic1.bmp->Canvas->TextOutA(x,y+=i,AnsiString().sprintf("a = %i px",aa));
pic1.bmp->Canvas->TextOutA(x,y+=i,AnsiString().sprintf("b = %i px",bb));
pic1.bmp->Canvas->TextOutA(x,y+=i,AnsiString().sprintf("upper = %i px",l0));
pic1.bmp->Canvas->TextOutA(x,y+=i,AnsiString().sprintf("lower = %i px",l1));
pic1.bmp->Canvas->TextOutA(x,y+=i,AnsiString().sprintf("upper`= %.3lf px",ll0));
pic1.bmp->Canvas->TextOutA(x,y+=i,AnsiString().sprintf("lower`= %.3lf px",ll1));
pic1.bmp->Canvas->Brush->Style=bsSolid;

Это использует мой собственный класс изображения с участниками:

xs,ys разрешение изображения
p[y][x].dd пиксельный доступ как 32-битное целое число без знака как цвет
p[y][x].db[4] пиксельный доступ в виде 4 * 8-битного целого без знака в виде цветовых каналов

Вы можете посмотреть на picture::p член как простой 2D массив
```
union color
{
DWORD dd; WORD dw[2]; byte db[4];
int i; short int ii[2];
color(){}; color(color& a){ *this=a; }; ~color(){}; color* operator = (const color *a) { dd=a->dd; return this; }; /*color* operator = (const color &a) { ...copy... return this; };*/
};
int xs,ys;
color p[ys][xs];
Graphics::TBitmap *bmp; // VCL GDI Bitmap object you do not need this...
```
где каждая ячейка может быть доступна как 32-битный пиксель p[][].dd как 0xAABBGGRR или же 0xAARRGGBB не уверен, что сейчас. Также вы можете получить прямой доступ к каналам с помощью p [] []. Db [4] как 8-битных байтов.

bmp участник GDI растровое изображение так bmp->Canvas-> получить доступ ко всем GDI вещи, которые не важны для вас.

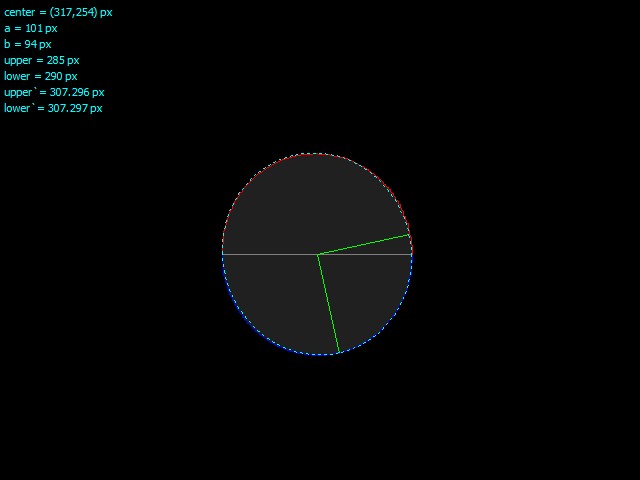
Вот результат для вашего второго изображения:

Серый горизонтальная линия — это дуга, проходящая через центр
Красно синий половинки дуги (перекрашиваются при подсчете)
зеленый являются базисными векторами полуосей
вода Тире-тире — это аналитическое наложение эллипса для сравнения.

Как видите, подгонка довольно близка (+/- 1 пиксель). Подсчитанные длины дуги upper,lower довольно близки к приблизительному среднему периметру окружности (окружности).

Вы должны добавить a0 проверка диапазона, чтобы решить, является ли начало верхней или нижней половиной, потому что нет гарантии, какую сторону главной оси это найдет. Интеграция обеих половин почти одинакова и насыщена на этапе интеграции 0.001*M_PI вокруг 307.3 pixels на длину дуги, которая только 17 а также 22 Отличие пикселей от прямого числа пикселей, которое даже лучше, чем я ожидаю, из-за псевдонимов …

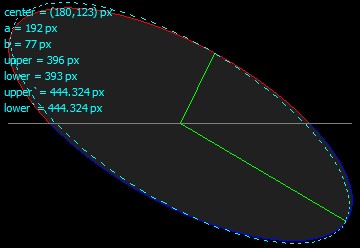
Для более эксцентричных эллипсов подгонка не так хороша, но результаты все еще достаточно хороши:

2