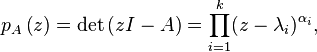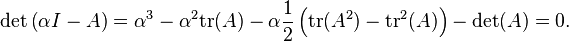Как найти самый большой собственный вектор матрицы?
Я пытаюсь реализовать это безуспешно, и я должен сделать это без использования внешних модулей numpy и т. Д. В приложении есть 3 модуля, которые я кодирую, Python и C #, C ++, но нет других модных библиотек, кроме стандартных.
В отдельном приложении я использовал svd numpy, и он работает очень точно. Поэтому я использую его, чтобы соответствовать моим результатам. Мой метод PCA, и до этого момента все было хорошо. Но после того, как я вычислил свою симметричную ковариационную матрицу, я не знаю, как найти самый большой собственный вектор.
Набор данных всегда 3d-точки, x, y и z.
vector center;
for(point p in points):
center += p;
center /= points.count;
sumxx = 0;
sumxy = 0;
sumxz = 0;
sumyy = 0;
sumyz = 0;
sumzz = 0;
for(point p in points):
vector s = p - center;
sumxx += s.x * s.x;
sumxy += s.x * s.y;
sumxz += s.x * s.z;
sumyy += s.y * s.y;
sumyz += s.y * s.z;
sumzz += s.z * s.z;
matrix3 mat = invert(matrix3(sumxx, sumxy, sumxz, sumxy, sumyy, sumyz, sumxz, sumyz, sumzz));
vector n;
if (determinant(mat) > 0)
normal = find_largest_eigenvalue
Решение
Давайте повторим то, что вы просите, чтобы уточнить:
- Найти собственный вектор матрицы
mat - Этот собственный вектор должен быть связан с наибольшим собственным значением матрицы
- Матрица является симметричной ковариационной матрицей Анализ главных компонентов. В частности, это симметрично.
- Ваша матрица квадратная размером 3 на 3, как показано в вашем коде
matrix3 mat = ...и подтверждено в (теперь удаленном) комментарии.
При этих очень специфических обстоятельствах применяется следующий ответ. Однако tmyklebu предостерегает от численной нестабильности этого подхода для некоторых патологических матриц, как правило, когда r близко к -1,
Хорошо, давайте начнем с небольшого чтения из страница википедии о характеристических многочленах
В линейной алгебре характеристический многочлен квадратной матрицы является многочленом, который инвариантен относительно подобия матрицы и имеет собственные значения в качестве корней.
бла-бла-бла, давайте перейдем непосредственно к Раздел матрицы 3х3 на странице алгоритмов собственных значений.
Если A является матрицей 3 × 3, то ее характеристическое уравнение может быть выражено как:
После нескольких строк (более или менее) этот псевдокод, для симметричных матриц (что, как вы говорите, есть, если я не ошибаюсь — в противном случае у вас могут быть сложные собственные значения):
p1 = A(1,2)^2 + A(1,3)^2 + A(2,3)^2
if (p1 == 0)
% A is diagonal.
eig1 = A(1,1)
eig2 = A(2,2)
eig3 = A(3,3)
else
q = (A(1,1) + A(2,2) + A(3,3)) / 3
p2 = (A(1,1) - q)^2 + (A(2,2) - q)^2 + (A(3,3) - q)^2 + 2 * p1
p = sqrt(p2 / 6)
B = (1 / p) * (A - q * I) % I is the identity matrix
r = determinant(B) / 2
% In exact arithmetic for a symmetric matrix -1 <= r <= 1
% but computation error can leave it slightly outside this range.
if (r <= -1)
phi = pi / 3
elseif (r >= 1)
phi = 0
else
phi = acos(r) / 3
end
% the eigenvalues satisfy eig3 <= eig2 <= eig1
eig1 = q + 2 * p * cos(phi)
eig3 = q + 2 * p * cos(phi + (2*pi/3))
eig2 = 3 * q - eig1 - eig3 % since trace(A) = eig1 + eig2 + eig3
end
Так ты хочешь max(eig1,eig2,eig3) в первом случае, eig1 во втором случае. Давайте позвоним e это самое большое собственное значение.
Для собственного вектора вы можете теперь просто решить (A-e*I)x=0
Другие решения
Существуют разные алгоритмы нахождения собственных значений. Некоторые из них работают от самых маленьких до самых больших, например QR; другие работают от самых больших до самых маленьких, например, степенная итерация или Якоби-Дэвидсон.
Возможно, вам нужен переключатель алгоритма. Попробуйте метод питания и посмотрите, поможет ли это.